Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
\(y'=-\frac{4}{\left(x-2\right)^2}\Rightarrow\left\{{}\begin{matrix}y'\left(3\right)=-4\\y\left(3\right)=6\end{matrix}\right.\)
Pt tiếp tuyến: \(y=-4\left(x-3\right)+6\Leftrightarrow y=-4x+18\)
b.
\(y'=\frac{-5}{\left(x-1\right)^2}\)
Tiếp tuyến song song với \(y=-5x-3\) nên có hệ số góc \(k=-5\)
\(\Rightarrow\frac{-5}{\left(x-1\right)^2}=-5\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn

Câu 1:
\(y=x^3-3x^2-2\Rightarrow y'=3x^2-6x\)
Gọi hoành độ của M là \(x_M\)
Hệ số góc của tiếp tuyến của đồ thị (C) tại M bằng 9 tương đương với:
\(f'(x_M)=3x_M^2-6x_M=9\)
\(\Leftrightarrow x_M=3\) hoặc $x_M=-1$
\(\Rightarrow y_M=-2\) hoặc \(y_M=-6\)
Vậy tiếp điểm có tọa độ (3;-2) hoặc (-1;-6)
Đáp án B
Câu 2:
Gọi hoành độ tiếp điểm là $x_0$
Hệ số góc của tiếp tuyến tại tiếp điểm là:
\(f'(x_0)=x_0^2-4x_0+3\)
Vì tt song song với \(y=3x-\frac{20}{3}\Rightarrow f'(x_0)=3\)
\(\Leftrightarrow x_0^2-4x_0+3=3\Leftrightarrow x_0=0; 4\)
Khi đó: PTTT là:
\(\left[{}\begin{matrix}y=3\left(x-0\right)+f\left(0\right)=3x+4\\y=3\left(x-4\right)+f\left(4\right)=3x-\dfrac{20}{3}\end{matrix}\right.\) (đt 2 loại vì trùng )
Do đó \(y=3x+4\Rightarrow \) đáp án A
Câu 3:
PT hoành độ giao điểm:
\(\frac{2x+1}{x-1}-(-x+m)=0\)
\(\Leftrightarrow x^2+(1-m)x+(m+1)=0\) (1)
Để 2 ĐTHS cắt nhau tại hai điểm pb thì (1) phải có hai nghiệm phân biệt
\(\Leftrightarrow \Delta=(1-m)^2-4(m+1)> 0\)
\(\Leftrightarrow m^2-6m-3> 0\)
\(\Leftrightarrow\left[{}\begin{matrix}m< 3-2\sqrt{3}\\m>3+2\sqrt{3}\end{matrix}\right.\)
Kết hợp với m nguyên và \(m\in (0;10)\Rightarrow m=7;8;9\)
Có 3 giá trị m thỏa mãn.

1.
Tiếp tuyến vuông góc với \(y=-x+2017\) nên có hệ số góc \(k=\frac{-1}{-1}=1\)
\(y'=3x^2-4x+2=1\)
\(\Rightarrow3x^2-4x+1=0\Rightarrow\left[{}\begin{matrix}x=1\\x=\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow x_1+x_2=1+\frac{1}{3}=\frac{4}{3}\)
2.
Tiếp tuyến song song Ox nên có hệ số góc \(k=0\)
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
3.
\(y'=x^2+6x=-9\Rightarrow\left(x+3\right)^2=0\Rightarrow x=-3\Rightarrow y=16\)
Pt tiếp tuyến: \(y=-9\left(x+3\right)+16=-9x-11\)
4.
Tiếp tuyến vuông góc \(y=\frac{1}{9}x+2017\) có hệ số góc \(k=\frac{-1}{\frac{1}{9}}=-9\)
\(y'=-3x^2+6x=-9\Leftrightarrow3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
Có 2 tiếp điểm nên có 2 tiếp tuyến thỏa mãn

Câu 1:
\(f'\left(1\right)=g'\left(1\right)=k\)
\(h\left(x\right)=\frac{f\left(x\right)+2}{g\left(x\right)+1}\Rightarrow h'\left(x\right)=\frac{f'\left(x\right)\left[g\left(x\right)+1\right]-g'\left(x\right)\left[f\left(x\right)+2\right]}{\left[g\left(x\right)+1\right]^2}\)
\(\Rightarrow h'\left(1\right)=\frac{k\left(b+1\right)-k\left(a+2\right)}{\left(b+1\right)^2}=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\)
Mà \(h'\left(1\right)=k\Rightarrow k=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\Rightarrow\frac{b-a-1}{\left(b+1\right)^2}=1\)
\(\Leftrightarrow b-a-1=\left(b+1\right)^2\Rightarrow a=b-1-\left(b+1\right)^2\)
\(\Rightarrow a=-b^2-b-2\)
Câu 2:
\(y=f\left(x\right)=\frac{x+1}{x-2}\Rightarrow f'\left(x\right)=\frac{-3}{\left(x-2\right)^2}\)
Phương trình hoành độ giao điểm:
\(\frac{x+1}{x-2}=x+m\Leftrightarrow x+1=\left(x+m\right)\left(x-2\right)\)
\(\Leftrightarrow x^2+\left(m-3\right)x-2m-1=0\)
\(\Delta=\left(m-3\right)^2+4\left(2m+1\right)=\left(m+1\right)^2+12>0\)
\(\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt A và B có hoành độ giả sử là a và b
Theo Viet: \(\left\{{}\begin{matrix}a+b=3-m\\ab=-3m-1\end{matrix}\right.\) \(\Rightarrow3a+3b-ab=10\) (1)
Mặt khác do tiếp tuyến tại A và B song song
\(\Leftrightarrow\frac{-3}{\left(a-2\right)^2}=\frac{-3}{\left(b-2\right)^2}\Leftrightarrow\left[{}\begin{matrix}a-2=b-2\\a-2=2-b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4-b\end{matrix}\right.\)
TH1: \(a=b\) thay vào (1):
\(\Rightarrow-a^2+6a-10=0\left(vn\right)\)
TH2: \(a=4-b\)
\(\Rightarrow a+b=4\Rightarrow3-m=4\Rightarrow m=-1\)

1.
Để ĐTHS có 2 tiệm cận thì \(m\ne-3\)
Khi đó:
\(\lim\limits_{x\rightarrow\infty}\frac{mx-3}{x+1}=m\Rightarrow y=m\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow-1}\frac{mx-3}{x+1}=\infty\Rightarrow x=-1\) là tiệm cận đứng
Giao điểm 2 tiệm cận có tọa độ \(A\left(-1;m\right)\)
Để A thuộc \(y=x+3\Leftrightarrow m=-1+3\Rightarrow m=2\)
2.
\(\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{x-2}}{x^2-4}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow2}\frac{\sqrt{x-2}}{x^2-4}=\infty\Rightarrow x=2\) là 1 TCĐ
\(x=-2\) ko thuộc TXĐ nên ko phải là tiệm cận
Vậy ĐTHS có 2 tiệm cận
3.
Để ĐTHS có đúng 2 TCĐ \(\Leftrightarrow x^2-mx+5=0\) có 2 nghiệm pb khác 1
\(\Leftrightarrow\left\{{}\begin{matrix}6-m\ne0\\\Delta=m^2-20>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne6\\\left[{}\begin{matrix}m\ge2\sqrt{5}\\m\le-2\sqrt{5}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{5;-5\right\}\)
Đề bài sai hoặc đáp án sai

Ta có \(y'=-4x^3-2x\)
a) Vì tiếp tuyến vuông góc với đường thẳng \(d:y=\frac{1}{6}x-\frac{1}{6}\)
Suy ra \(y'\left(x_0\right)=-6\Leftrightarrow2x_0^3+x_0^2-3=0\Leftrightarrow x_0=1\Rightarrow y_0=-3\)
Phương trình tiếp tuyến là \(y=-6x+3\)
b) Vì tuyến tuyến song song với đường thẳng \(y=6x+2\) nên ta có :
\(y'\left(x_0\right)=6\Leftrightarrow2x_0^3+x_0^2+3=0\Leftrightarrow\left(x_0+1\right)\left(2x_0^2-2x_0+3\right)=0\Rightarrow x_0=-1\Rightarrow y_0=-3\)
Nên ta có phương trình tiếp tuyến là :
\(y=6\left(x+1\right)-3=6x+3\)
2x mũ 3 cộng x ũ 2 cộng 3 bằng 0 là ban lấy ở đâu đó ạ mình không hiểu

1.
\(\lim\limits_{x\rightarrow\infty}\frac{3x-2}{x+1}=3\Rightarrow y=3\) là tiệm cận ngang
2.
\(\lim\limits_{x\rightarrow2}\frac{-2x}{x-2}=\infty\Rightarrow x=2\) là tiệm cận đứng
3.
\(\lim\limits_{x\rightarrow\infty}\frac{x-2}{x^2-1}=0\Rightarrow y=0\) là tiệm cận ngang
4.
\(\lim\limits_{x\rightarrow\infty}\frac{x-1}{x^2-x}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow0}\frac{x-1}{x^2-x}=\infty\Rightarrow x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{x-1}{x^2-x}=1\) hữu hạn nên \(x=1\) ko phải tiệm cận đứng
ĐTHS có 2 tiệm cận

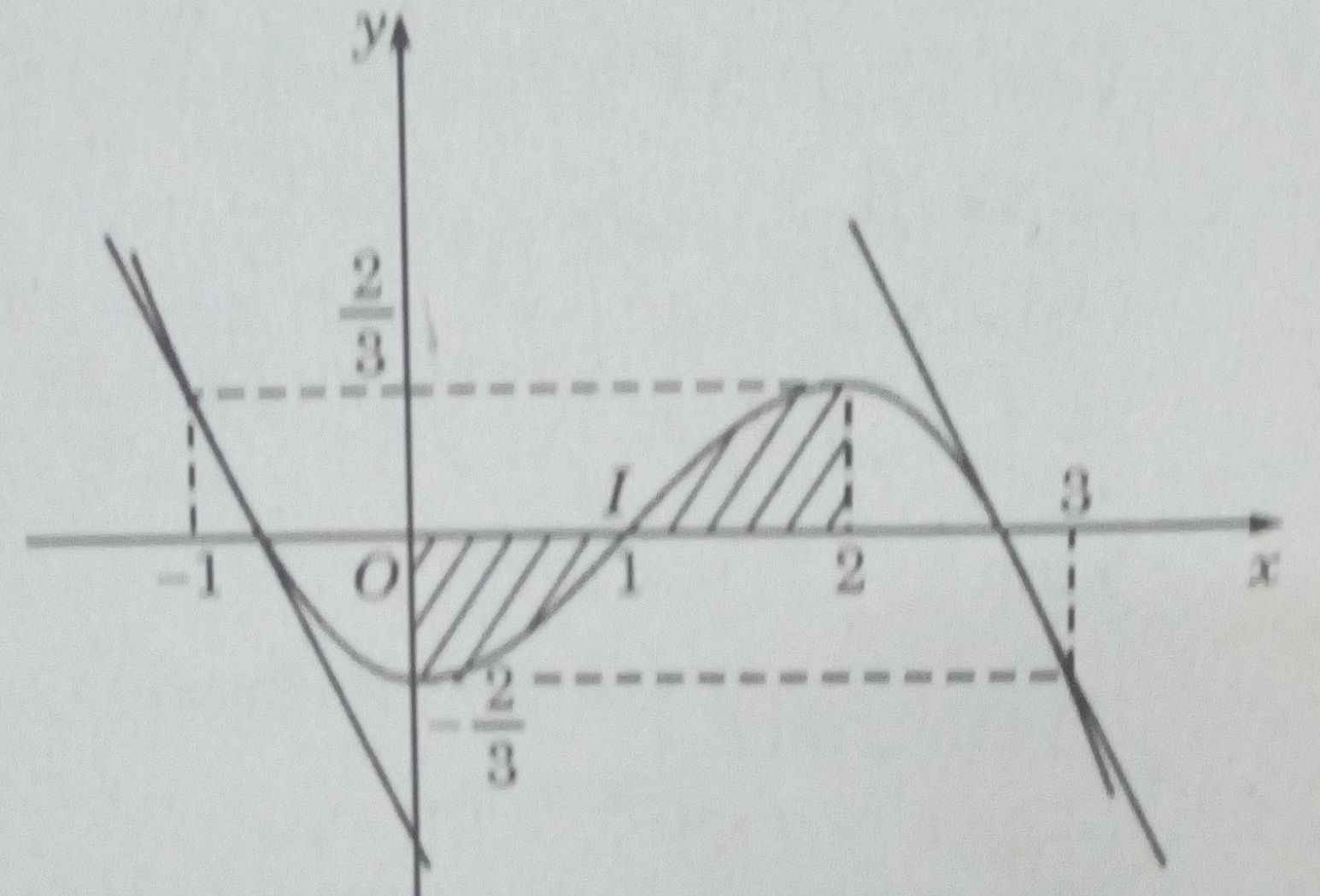

Đáp án D
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là: y = f'(x0).(x - x0) + y0
Cách giải:
Tiếp tuyến của (C) vuông góc với đường thẳng d: y = x nên tiếp tuyến có hệ số góc k = -1
=> Phương trình tiếp tuyến
=> Phương trình tiếp tuyến