Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)

Ta có: \(\widehat{A}=\frac{q}{3}\widehat{C}\).
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+80^o+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+\widehat{C}=180^o-80^o=100^o\)
=> \(\widehat{C}\left(q+3\right)=300^o\)
=> \(\widehat{C}=\frac{300^o}{q+3}\)
=> \(\widehat{A}=\frac{q}{3}.\frac{300^o}{q+3}=\frac{100^oq}{q+3}\)

Bạn tự vẽ hình nghen
Vì AD là phân giác của \(\widehat{BAC}\) nên \(\widehat{BAD}=\widehat{DAC}=30\) độ
Ta có SABD=\(\frac{1}{2}\times AB\times AD\times\sin\widehat{BAD}\) (1)
SADC=\(\frac{1}{2}\times AD\times AC\times\sin\widehat{DAC}\) (2)
SABC=\(\frac{1}{2}\times AB\times AC\times\sin\widehat{BAC}\) (3)
từ (1),(2) và (3) , ta suy ra:\(\frac{1}{2}AD\times\left(AB+AC\right)\times\sin30=AB\times AC\times\sin60\)
\(\Rightarrow AD\times\frac{1}{2}\times12\sqrt{3}=96\times\frac{\sqrt{3}}{2}\)\(\Rightarrow AD=8\)
Vậy AD=8(đvd)

Thay a,b,c lần lượt vào biểu thức...
Tính được kết quả:
a) A= \(-\frac{7}{10}\)
b) B= \(-\frac{2}{7}\)
c) C= 0

chứng minh được AH=BH -> SA= SB _> tam giác SAB cân ở S
gọi M là trung điểm của AB -> SM vuông góc với AB -> góc giữa mp (SAB) và mp (ABC) là góc SMH -> góc SMH = 60 độ
-> tìm được SH -> tìm được thể tích
tìm diên tích tam giác SAB -> khoảng cách từ C đến mp (SAB)
Vì I là trung điểm của SC nên khoảng cách từ I đến mp (SAB) bằng một nửa khoảng cách từ C đến mp (SAB)

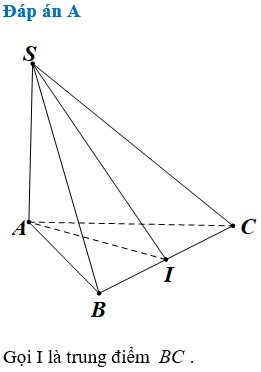
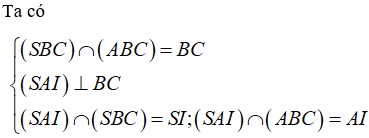
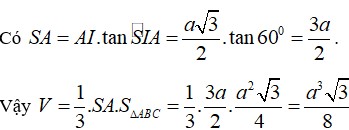
Đáp án là B.
V S . A B C = 1 3 S A . S Δ A B C = 1 3 . a 3 . a 2 3 4 = a 3 4 .