K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

VT
22 tháng 9 2019
Hướng dẫn: Chọn đáp án B
Kinh nghiệm: Bài toán cho x1 và xu hướng đang tăng (v1 > 0) hoặc đang giảm (v1 <0) thì nên làm theo cách 2.
Cách 1: Viết lại phương trình li độ vận tốc:
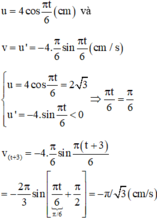
Cách 2: Chọn trạng thái tại thời điểm t1 là trạng thái ban đầu Þj= p/6 Pha dao động ở thời điểm tiếp theo:
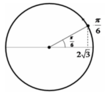
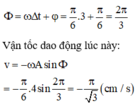

9 tháng 6 2015
Bước sóng: lamda = v/f = 20/2 = 10cm.
M cách O 1 đoạn 40cm = 4 lamda, nên M dao động cùng pha với O.
Vậy li độ của M bằng li độ của O, bằng căn 3 mm.

VT
14 tháng 4 2019
Hướng dẫn: Chọn đáp án B
Kinh nghiệm: Bài toán cho v1 thì nên làm theo cách 1.
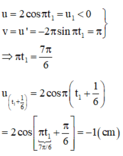

VT
29 tháng 8 2018
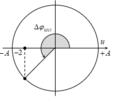
+ Độ lệch pha giữa hai điểm M và O là
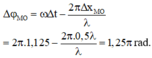
→ Biểu diễn dao động của điểm O và M tương ứng trên đường tròn. Tại thời điểm ban đầu điểm O đang ở vị trí biên dương.
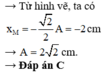
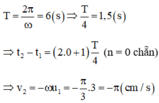

a. Theo giả thiết: \(x_1=4\cos(\dfrac{\pi}{6}t_1)=2\sqrt 3\) và $x$ đang giảm, nên ta biểu diễn dao động này bằng véc tơ quay:
> M x 4 30 O N -2
Thời điểm $t_1$, véc tơ quay tại vị trí M.
Sau thời điểm $t_1$ một khoảng $\Delta t = 3s$, véc tơ quay đã quay 1 góc là:
\(\alpha = \omega.t = \dfrac{\pi}{6}.3=\dfrac{\pi}{2}(rad)\)
Lúc này, véc tơ quay đã quay đến N. Từ giản đồ véc tơ ở trên ta suy ra li độ: $x = -2cm$
b. Bước sóng: \(\lambda=v.t=2.12=24cm\)
Điểm M trễ pha hơn O là: \(\Delta \varphi = \dfrac{2\pi.d}{\lambda}=\dfrac{2\pi.40}{24}=\dfrac{10\pi}{3}(rad)\)
Biểu diễn trạng thái dao động của M theo O ở thời điểm $t_1$ trên giản đồ véc tơ, ta có:
O M > x 4
Từ giản đồ trên dễ dàng suy được li độ của M là \(-2\sqrt 3cm\)