Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B=\(\dfrac{10^9+1}{10^{10}+1}< \dfrac{10^5+1+9}{10^{10}+1+9}=\dfrac{10^9+10}{10^{10}+10}=\dfrac{10.\left(10^8+1\right)}{10\left(10^9+1\right)}\)
= A


Ta có F < 1 nên
\(\dfrac{13580}{34569}< 1< \dfrac{13580+\left(-1\right)}{34569+\left(-1\right)}=\dfrac{13579}{34568}\)<\(\dfrac{13579}{34567}\)
Từ đó suy ra \(\dfrac{13580}{34569}< \dfrac{13579}{34567}\)hay\(\dfrac{13579}{34567}>\dfrac{13580}{34569}\)
Vậy E > F

a, \(A-B=\frac{3}{8^3}+\frac{7}{8^4}-\frac{7}{8^3}-\frac{3}{8^4}==\left(\frac{7}{8^4}-\frac{3}{8^4}\right)-\left(\frac{7}{8^3}-\frac{3}{8^3}\right)=\frac{4}{8^4}-\frac{4}{8^3}< 0\)
Vậy A < B
b, \(A=\frac{10^7+5}{10^7-8}=\frac{10^7-8+13}{10^7-8}=1+\frac{13}{10^7-8}\)
\(B=\frac{10^8+6}{10^8-7}=\frac{10^8-7+13}{10^8-7}=1+\frac{13}{10^8-7}\)
Vì \(10^7-8< 10^8-7\Rightarrow\frac{1}{10^7-8}>\frac{1}{10^8-7}\Rightarrow\frac{13}{10^7-8}>\frac{13}{10^8-7}\Rightarrow A>B\)
c,Áp dụng nếu \(\frac{a}{b}>1\Rightarrow\frac{a}{b}>\frac{a+n}{a+n}\) có:
\(B=\frac{10^{1993}+1}{10^{1992}+1}>\frac{10^{1993}+1+9}{10^{1992}+1+9}=\frac{10^{1993}+10}{10^{1992}+10}=\frac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}=\frac{10^{1992}+1}{10^{1991}+1}=A\)
Vậy A < B


\(\dfrac{a}{b}< 1\Leftrightarrow\dfrac{a}{b}< \dfrac{a+m}{b+m}\)\(\left(a,b,m\in N\cdot\right)\)
Ta có:
\(B=\dfrac{10^9+1}{10^{10}+1}< 10\left(10^9< 10^{10}\right)\)
\(\Leftrightarrow B=\dfrac{10^9+1}{10^{10}+1}< \dfrac{10^9+1+9}{10^{10}+1+9}=\dfrac{10^9+10}{10^{10}+10}=\dfrac{10\left(10^8+1\right)}{10\left(10^9+1\right)}=\dfrac{10^8+1}{10^9+1}=A\)
\(\Leftrightarrow A>B\)

b: \(A=\dfrac{10^7-8+13}{10^7-8}=1+\dfrac{13}{10^7-8}\)
\(B=\dfrac{10^8-7+13}{10^8-7}=1+\dfrac{13}{10^8-7}\)
mà \(10^7-8< 10^8-7\)
nên A>B
c: \(\dfrac{1}{10}A=\dfrac{10^{1992}+1}{10^{1992}+10}=1-\dfrac{9}{10^{1992}+10}\)
\(\dfrac{1}{10}B=\dfrac{10^{1993}+1}{10^{1993}+10}=1-\dfrac{9}{10^{1993}+10}\)
mà \(\dfrac{9}{10^{1992}+10}>\dfrac{9}{10^{1993}+10}\)
nên A<B

d, Vì B=10^1993+1/10^1992+1 > 1 =>10^1993+1/10^1992+1>10^1993+1+9/10^1992+1+9 = 10^1993+10/10^1992+10= 10. (10^1992+1)/10. (10^1991+1) = 10^1992+1/10^1991+1=A Vậy A=B
cau d B>1 ta co tinh chat (\(\dfrac{a}{b}>\dfrac{a+m}{b+m}\) ) B> \(\dfrac{10^{1993}+1+9}{10^{1992}+1+9}\)\(=\dfrac{10^{1993}+10}{10^{1992}+10}\)=\(\dfrac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}\)=\(\dfrac{10^{1992}+1}{10^{1991}+1}\)=A
Suy ra B>A(chuc ban hoc goi nhe)

\(A=\dfrac{8^9+13}{8^9+7}=\dfrac{8^9+7+6}{8^9+7}=1+\dfrac{6}{8^9+7}\)
\(B=\dfrac{8^{10}-1+5}{8^{10}-1}=1+\dfrac{5}{8^{10}-1}\)
Vì \(1+\dfrac{6}{8^9+7}>1+\dfrac{5}{8^{10}-1}\) \(\Rightarrow A>B\)

Ta có:
\(10A=10.\dfrac{10^7+1}{10^8+1}=\dfrac{10.10^7+1}{10^8+1}=\dfrac{10^8+1}{10^8+1}=1\)
\(10B=\dfrac{10.10^8+1}{10^9+1}=\dfrac{10^9+1}{10^9+1}=1\)
\(\Rightarrow10A=10B\)
\(\Rightarrow A=B\)
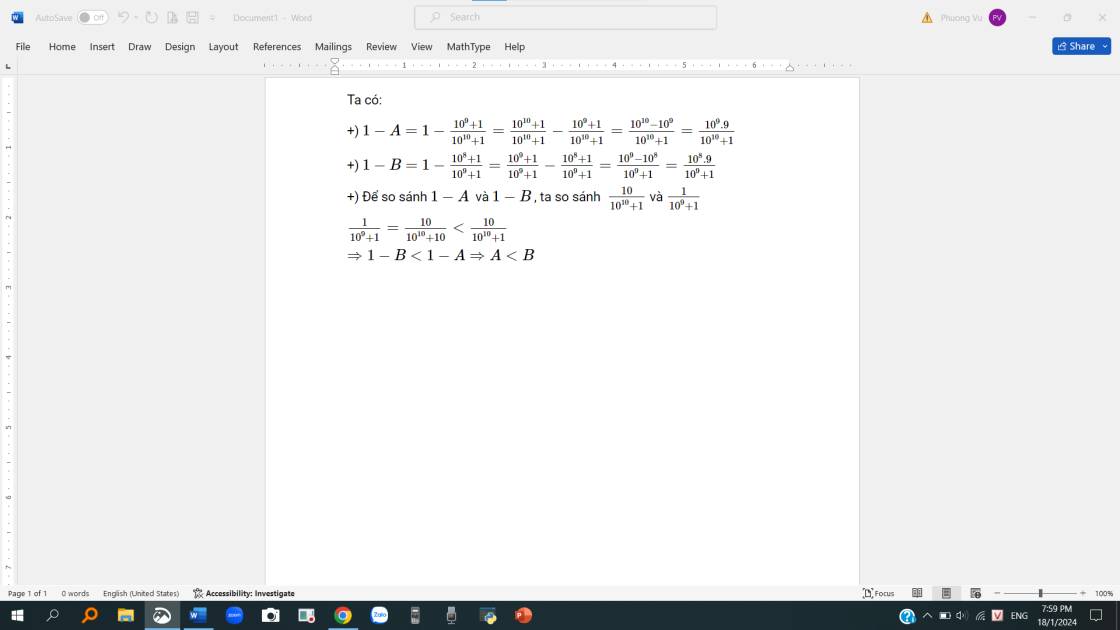
b: \(10A=\dfrac{10^9+10}{10^9+1}=1+\dfrac{9}{10^9+1}\)
\(10B=\dfrac{10^{10}+10}{10^{10}+1}=1+\dfrac{9}{10^{10}+1}\)
Vì \(10^9+1< 10^{10}+1\)
nên \(\dfrac{9}{10^9+1}>\dfrac{9}{10^{10}+1}\)
=>\(1+\dfrac{9}{10^9+1}>1+\dfrac{9}{10^{10}+1}\)
=>10A>10B
=>A>B