Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có : \(\log_25=\log_23.\log_35=ab\)
\(\Rightarrow I=\log_{140}63=\frac{\log_263}{\log_2140}=\frac{\log_2\left(3^2.7\right)}{\log_2\left(2^2.5.7\right)}=\frac{2\log_23+\log_27}{2+\log_25+\log_27}=\frac{2a+c}{2+ab+c}\)
Chọn 2 làm cơ số, ta có :
\(A=\log_616=\frac{\log_216}{\log_26}=\frac{4}{1=\log_23}\)
Mặt khác :
\(x=\log_{12}27=\frac{\log_227}{\log_212}=\frac{3\log_23}{2+\log_23}\)
Do đó : \(\log_23=\frac{2x}{3-x}\) suy ra \(A=\frac{4\left(3-x\right)}{3+x}\)
b) Ta có :
\(B=\frac{lg30}{lg125}=\frac{lg10+lg3}{3lg\frac{10}{2}}=\frac{1+lg3}{3\left(1-lg2\right)}=\frac{1+a}{3\left(1-b\right)}\)
c) Ta có :
\(C=\log_65+\log_67=\frac{1}{\frac{1}{\log_25}+\frac{1}{\log_35}}+\frac{1}{\frac{1}{\log_27}+\frac{1}{\log_37}}\)
Ta tính \(\log_25,\log_35,\log_27,\log_37\) theo a, b, c .
Từ : \(a=\log_{27}5=\log_{3^3}5=\frac{1}{3}\log_35\)
Suy ra \(\log_35=3a\) do đó :
\(\log_25=\log_23.\log35=3ac\)
Mặt khác : \(b=\log_87=\log_{2^3}7=\frac{1}{3}\log_27\) nên \(\log_27=3b\)
Do đó : \(\log_37=\frac{\log_27}{\log_23}=\frac{3b}{c}\)
Vậy : \(C=\frac{1}{\frac{1}{3ac}+\frac{1}{3a}}+\frac{1}{\frac{1}{3b}+\frac{c}{3b}}=\frac{3\left(ac+b\right)}{1+c}\)
d) Điều kiện : \(a>0;a\ne0;b>0\)
Từ giả thiết \(\log_ab=\sqrt{3}\) suy ra \(b=a^{\sqrt{3}}\). Do đó :
\(\frac{\sqrt{b}}{a}=a^{\frac{\sqrt{3}}{2}-1};\frac{\sqrt[3]{b}}{\sqrt{a}}=a^{\frac{\sqrt{3}}{3}-\frac{1}{2}}=a^{\frac{\sqrt{3}}{3}\left(\frac{\sqrt{3}}{2}-1\right)}\)
Từ đó ta tính được :
\(A=\log_{a^{\alpha}}a^{\frac{-\sqrt{3}}{3}\alpha}=\log_{a^{\alpha}}\left(a^{\alpha}\right)^{\frac{-\sqrt{3}}{3}}=\frac{-\sqrt{3}}{3}\) với \(\alpha=\frac{\sqrt{3}}{2}-1\)
Ta có :
\(a=\log_615=\frac{\log_215}{\log_26}=\frac{\log_23+\log_25}{1+\log_23}\left(1\right)\)
\(b=\log_{12}18=\frac{\log_118}{\log_212}=\frac{\log_2\left(2.3^2\right)}{\log_2\left(2^2.3\right)}=\frac{1+2\log_23}{2+\log_23}\left(2\right)\)
Từ \(\left(2\right)\Rightarrow b\left(2+\log_23\right)=1+2\log_23\Leftrightarrow\left(b-2\right)\log_23=1-2b\Leftrightarrow\log_23=\frac{1-2b}{b-2}\)
Từ \(\left(1\right)\Rightarrow\log_25=a\left(a+\log_23\right)-\log_23=\left(a-1\right)\log_23+a=\left(a-1\right)\frac{1-2b}{b-2}+a=\frac{b-5}{4b-2a-2ab-2}\)
\(\Rightarrow F=\log_{25}24=\frac{\log_224}{\log_225}=\frac{\log_2\left(2^3.3\right)}{\log_25^2}=\frac{3+\log_23}{2\log_25}=\frac{3+\frac{1-2b}{b-2}}{2.\frac{2b-a-ab-1}{b-2}}=\frac{b-5}{4b-2a-2ab-2}\)
Ta có \(a=\log_{25}7=\frac{\log_27}{\log_225}=\frac{\log_27}{2\log_25}=\frac{\log_27}{2b}\Rightarrow\log_27=2ab\)
\(\Rightarrow H=\log_{\sqrt[3]{5}}\frac{49}{8}=\frac{\log_2\frac{49}{8}}{\log_2\sqrt[3]{5}}=\frac{\log_2\frac{7^2}{2^2}}{\log_25^{\frac{1}{3}}}=\frac{2\log_27-3}{\frac{1}{3}\log_25}=\frac{12ab-9}{b}\)
a) \(log_3\dfrac{6}{5}>log_3\dfrac{5}{6}\) vì \(\dfrac{6}{5}>\dfrac{5}{6}\)
b) \(log_{\dfrac{1}{3}}9>log_{\dfrac{1}{3}}17\) vì \(9>17\) và \(0< \dfrac{1}{3}< 1\).
c) \(log_{\dfrac{1}{2}}e>log_{\dfrac{1}{2}}\pi\) vì \(e>\pi\) và \(0< \dfrac{1}{2}< 1\)
d) \(log_2\dfrac{\sqrt{5}}{2}>log_2\dfrac{\sqrt{3}}{2}\) vì \(\dfrac{\sqrt{5}}{2}>\dfrac{\sqrt{3}}{2}\).
Em rất muốn biết ... anh học lớp mấy vậy ??? Đây là bài lớp 12 mà 
Ta có : \(b=lg2=lg\left(\frac{10}{5}\right)=1-lg5\Rightarrow lg5=1-b\)
\(\Rightarrow G=\log_{125b}30=\frac{lg30}{lg125}=\frac{lg\left(3.10\right)}{lg\left(5^3\right)}=\frac{1+lg3}{3lg5}=\frac{1+a}{3\left(1-b\right)}\)
Ta có :
\(\begin{cases}a=\log_{27}5=\frac{\log_25}{\log_227}=\frac{\log_25}{3\log_23}=\frac{\log_25}{3c}\Rightarrow\log_25=3ac\\b=\log_87=\frac{\log_27}{\log_28}=\frac{\log_27}{3}\Rightarrow\log_27=3b\end{cases}\)
\(\Rightarrow J=\log_635=\frac{\log_235}{\log_26}=\frac{\log_25+\log_27}{1+\log_23}=\frac{3ac+3b}{1+c}\)
a) Ta có \(\log_32<\log_33=1=\log_22<\log_23\)
b) \(\log_23<\log_24=2=\log_39<\log_311\)
c) Đưa về cùng 1 lôgarit cơ số 10, ta có
\(\frac{1}{2}+lg3=\frac{1}{2}lg10+lg3=lg3\sqrt{10}\)
\(lg19-lg2=lg\frac{19}{2}\)
So sánh 2 số \(3\sqrt{10}\) và \(\frac{19}{2}\) ta có :
\(\left(3\sqrt{10}\right)^2=9.10=90=\frac{360}{4}<\frac{361}{4}=\left(\frac{19}{2}\right)^2\)
Vì vậy : \(3\sqrt{10}<\frac{19}{2}\)
Từ đó suy ra \(\frac{1}{2}+lg3\)<\(lg19-lg2\)
d) Ta có : \(\frac{lg5+lg\sqrt{7}}{2}=lg\left(5\sqrt{7}\right)^{\frac{1}{2}}=lg\sqrt{5\sqrt{7}}\)
Ta so sánh 2 số : \(\sqrt{5\sqrt{7}}\) và \(\frac{5+\sqrt{7}}{2}\)
Ta có :
\(\sqrt{5\sqrt{7}}^2=5\sqrt{7}\)
\(\left(\frac{5+\sqrt{7}}{2}\right)^2=\frac{32+10\sqrt{7}}{4}=8+\frac{5}{2}\sqrt{7}\)
\(8+\frac{5}{2}\sqrt{7}-5\sqrt{7}=8-\frac{5}{2}\sqrt{7}=\frac{16-5\sqrt{7}}{2}=\frac{\sqrt{256}-\sqrt{175}}{2}>0\)
Suy ra : \(8+\frac{5}{2}\sqrt{7}>5\sqrt{7}\)
Do đó : \(\frac{5+\sqrt{7}}{2}>\sqrt{5\sqrt{7}}\)
và \(lg\frac{5+\sqrt{7}}{2}>\frac{lg5+lg\sqrt{7}}{2}\)
a) Bằng máy tính cầm tay ta tính được
log35 ≈ 1,464973521; log74 ≈ 0,7124143742,
điều này gợi ý ta tìm cách chứng minh log35 > 1 > log74.
Thật vậy, sử dụng tính chất của lôgarit và tính chất so sánh hai lũy thừa cùng cơ số ta có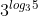
= 5 > 3 = 31 
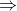log35 > 1.
Tương tự 71= 7> 4 =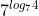
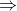1> log74. Từ đó log35 > log74.
b) Ta có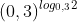
= 2 >1 =(o,3)0 
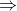log0,32 < 0
và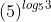
= 3 > 1 =50 
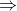log53 > 0.
Từ đó log0,32 < log53.
c)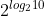
= 10 > 23 
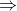log210 > 3 và 
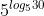= 30 < 53 
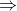log530 < 3, do đó log210 > log530.