K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 10 2021
\(5^{1999}>5^{1996}=\left(5^4\right)^{499}=625^{499}\)
21 tháng 10 2021
333444=(3334)111=(1114.81)111333444=(3334)111=(1114.81)111
444333=(4443)111=(1113.64)111444333=(4443)111=(1113.64)111
Dễ thấy 1114.81>1113.641114.81>1113.64
⇒333444>444333⇒333444>444333
21 tháng 10 2021
\(a,4^{333}=\left(4^3\right)^{111}=64^{111}< 81^{111}=\left(3^4\right)^{111}=3^{444}< 3^{445}\\ b,39^{15}>36^{15}=\left(6^2\right)^{15}=6^{30}\\ c,25^{45}=\left(5^2\right)^{45}=5^{90}< 5^{102}=\left(5^3\right)^{34}=125^{34}\)
N
4
AH
11 tháng 7 2018
(x+6)4=4096
(x+6)4=84
==> x+6=8 hoặc x+6=—8
==> x=8–6 hoặc x=—8–6
==> x= 2 hoặc x=—14
2x—3=128
2x—3=27
==> x—3=7
x=7+3
x=10
Ss: 22018 và 16900
Ta có 16900=(24)900=23600
Vì 22018<23600
Nên 22018<23600
MD
12 tháng 11 2017
a,5mũ 36=(5mũ3)mũ12=125 mũ12
11^24=(11^2)12=121^12
vì 121<125 nên 5^36>11^24
13 tháng 7 2018
\(2^{x-3}=128\Leftrightarrow2^{x-3}=2^7\Rightarrow x-3=7\Leftrightarrow x=10\)
\(\left(x+6\right)^4=4096\Leftrightarrow\left(x+6\right)^4=2^{12}=\left(2^3\right)^4=8^4\Rightarrow x+6=8\Leftrightarrow x=2\)
13 tháng 7 2018
\(2^{2018}=\left(2^4\right)^{504}.2^2==16^{504}.4< 16^{900}\\ \)
\(17^{20}>16^{20}=\left(4^2\right)^{20}=4^{40}\)
\(3^{444}=\left(3^4\right)^{111}=81^{111}>64^{111}=\left(4^3\right)^{111}=4^{333}\\ \)
VM
2
HT
12 tháng 10 2019
Đặt B =\(32^{17}.8^{19}\)
So sánh :\(A=64^{11}.16^{11}\)và \(B=32^{17}.8^{19}\)
TA có :\(A=64^{11}.16^{11}=\left(64.16\right)^{11}=1024^{11}=\left(2^{10}\right)^{11}\)\(=2^{110}\)
\(B=32^{17}.8^{19}=\left(2^5\right)^{17}.\left(2^3\right)^{19}=2^{85}.2^{57}\)\(=2^{142}\)
VÌ A < B ( 2110< 2142)
Nên A < 3217.819
14 tháng 6 2024
mọi người ơi cho mình hỏi tại sao: x mũ 2 nhân với 9 lại viết thành x nhân với 3 mũ 2 chứ ko phải x nhân với 9 mũ 2 vậy
PN
1
DD
Đoàn Đức Hà
Giáo viên
21 tháng 8 2021
\(\frac{10^{20}+1}{10^{22}+1}=\frac{10^{20}+\frac{1}{100}+\frac{99}{100}}{10^{22}+1}=\frac{1}{100}+\frac{99}{100\left(10^{22}+1\right)}\)
\(\frac{10^{22}+1}{10^{24}+1}=\frac{10^{22}+\frac{1}{100}+\frac{99}{100}}{10^{24}+1}=\frac{1}{100}+\frac{99}{100\left(10^{24}+1\right)}\)
Có \(10^{22}+1< 10^{24}+1\Rightarrow\frac{99}{100\left(10^{22}+1\right)}>\frac{99}{100\left(10^{24}+1\right)}\)
do đó \(\frac{10^{20}+1}{10^{22}+1}>\frac{10^{22}+1}{10^{24}+1}\).
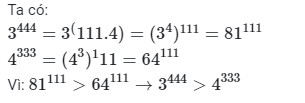
\(4^{115}=2^{230}\)
\(128^{24}=2^{168}\)
mà 230>168
nên \(4^{115}>128^{24}\)
4¹¹⁵= 16384¹⁰⁸
128²⁴= 16384²³
=> 4¹¹⁵ > 128²⁴