MR
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
7 tháng 12 2015
Bài này bạn đăng rồi Nguyễn Nhật Minh trả lời đúng rồi mà :
http://olm.vn/hoi-dap/question/314450.html
7 tháng 12 2015
1)
\(xy-y=x\Leftrightarrow y=\frac{x}{x-1}=1+\frac{1}{x-1}\)
y thuộc Z => x -1 thuộc U(1) ={ -1;1}
+x =-1 => y =0
+x =1 => y =2
2) \(x.\left(1-\frac{1}{7}\right)<1\frac{6}{7}\Leftrightarrow x.\frac{6}{7}<\frac{13}{7}\Rightarrow x<\frac{13}{7}.\frac{7}{6}=\frac{13}{6}=2,1\left(6\right)\)
x thuộc Z+ => x thuộc {1;2}
22 tháng 9 2015
1. \(\frac{x}{y}=\frac{7}{17}\)
3. Có 6 cặp
4. 0 có cặp nào hết
Câu 2 mình không biết nha. Thông cảm
TH
2
28 tháng 1 2017
\(\frac{x}{6}-\frac{1}{y}=\frac{1}{2}\)
\(\Rightarrow\frac{x}{6}-\frac{1}{2}=\frac{1}{y}\)
\(\Rightarrow\frac{x}{6}-\frac{3}{6}=\frac{1}{y}\)
\(\Rightarrow\frac{x-3}{6}=\frac{1}{y}\)
\(\Rightarrow\left(x-3\right)y=6\)
Ta có bảng sau:
...
NT
1
K
31 tháng 7 2016
\(\frac{5}{x}=\frac{1}{8}-\frac{y}{4}=\frac{1-2y}{8}\)
\(\Rightarrow x=5:\frac{1-2y}{8}=\frac{40}{1-2y}\)
Do x, y là số nguyên => 40 chia hết cho 1 - 2y
=> 1 - 2y thuộc Ư(40)
Mà 1 - 2y là lẻ => 1 - 2y thuộc {-1; 1; -5; 5}
=> y thuộc {1; 0; 3; -2}
=> x thuộc {-40; 40; -8; 8}
R
3
CE
1
HP
14 tháng 4 2016
\(\frac{5}{x}+\frac{y}{4}=\frac{1}{8}\)
\(\Rightarrow\frac{5}{x}=\frac{1}{8}-\frac{y}{4}=\frac{1}{8}-\frac{2y}{8}=\frac{1-2y}{8}\)
=>x.(1-2y)=5.8=40
=>x và 1-2y là ước của 40
2y là số chẵn =>1-2y là số lẻ =>1-2y là ước lẻ của 40
Ta có bảng sau:
| x | 40 | -40 | 8 | -8 |
| 1-2y | 1 | -1 | 5 | -5 |
suy ra :
| x | 40 | -40 | 8 | -8 |
| y | 0 | 1 | -2 | 3 |
Vậy.................................................
NN
5
13 tháng 3 2016
quy đồng lên bỏ mẫu ta có 160+8xy=4x
=> 4x-8xy=160
=4x(1-2y)=160
=x(1-2y)=40
1-2y thuộc Z => đó là số lẻ ước của 40 chỉ có 5 và -5 là số lẻ khỏi cần tính => có 2 cặp
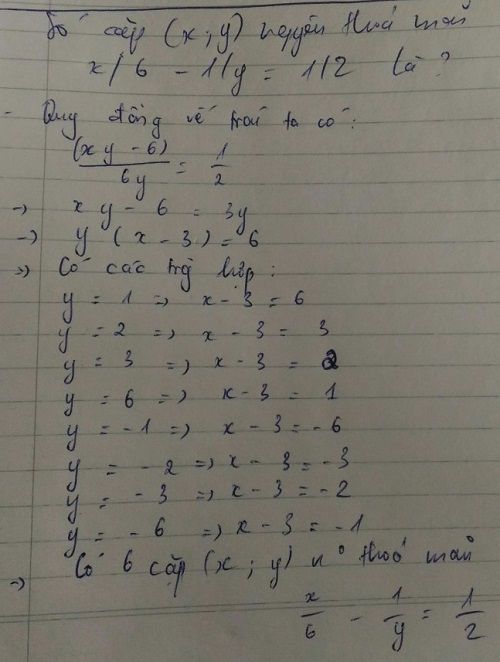
2(xy-6)=6y
(xy-6)=3y
x=(3y+6)/y=3+6/y
y={-6,-3,-2,-1,1,2,3,6)
x={2,1,0,-3,9,6,5,4)
\(\frac{x}{6}-\frac{1}{y}=\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{y}=\frac{x}{6}-\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{y}=\frac{x-3}{6}\)
\(\Leftrightarrow y\left(x-3\right)=6\)
=> y và x - 3 phải là ước của 6
=> Ư(6) = { - 6; - 3; - 2; - 1; 1; 2; 3; 6 }
Ta có bảng sau :
Vậy có 8 cặp số nguyên ( x;y ) thỏa mãn đề bài