Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
Kiểm tra:

Ta có thể viết được các tỉ số khác nhau cũng có thể "rút gọn" như vậy
Chẳng hạn:
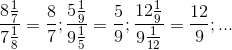

a.
\(\dfrac{9^3}{\left(3^4-3^3\right)^2}\\ =\dfrac{3^6}{\left(3^3\left(3-1\right)\right)^2}\\ =\dfrac{3^6}{\left(3^3.2\right)^2}\\ =\dfrac{3^6}{3^6.2^4}=\dfrac{1}{2^4}\)
b.
\(\dfrac{\left(5^4-5^3\right)^2}{1255}\\ =\dfrac{\left(5^3\left(5-1\right)\right)^2}{5.251}\\ =\dfrac{\left(5^3.4\right)^2}{5.251}\\ =\dfrac{5^6.4^2}{5.251}\\ =\dfrac{5^5.4^2}{251}\)
c.
\(\dfrac{32^5.81^4}{16^5.27^5}\\ =\dfrac{2^{25}.3^{16}}{2^{20}.3^{15}}\\ =2^5.3=32.3=96\)
f.
\(\dfrac{16^4-8^5}{48}=\dfrac{2^{16}-2^{15}}{2^4.3}\\ =\dfrac{2^{15}.\left(2-1\right)}{2^4.3}\\ =\dfrac{2^{15}}{2^4.3}\\ =\dfrac{2^{11}}{3}\)

Câu 2
(a+3)(b-4)-(a-3)(b+4)=0
=>ab-4a+3b-12-ab-4a+3b+12=0
=>-8a=-6b
=>a/b=3/4
=>a/3=b/4

Đặt \(A=\left(1+\dfrac{7}{9}\right)\left(1+\dfrac{7}{20}\right)\left(1+\dfrac{7}{33}\right)....\left(1+\dfrac{7}{2900}\right)\)
\(B=\left(81-\dfrac{3}{4}\right)\left(81-\dfrac{3^2}{5}\right)\left(81-\dfrac{3^3}{6}\right)....\left(81-\dfrac{3^{2014}}{2017}\right)\)
Ta có:
\(A=\left(1+\dfrac{7}{9}\right)\left(1+\dfrac{7}{20}\right)\left(1+\dfrac{7}{33}\right).....\left(1+\dfrac{7}{2900}\right)\)
\(A=\dfrac{16}{9}.\dfrac{27}{20}.\dfrac{40}{33}.....\dfrac{2907}{2900}\)
\(A=\dfrac{2.8}{1.9}.\dfrac{3.9}{2.10}.\dfrac{4.10}{3.11}.....\dfrac{51.57}{50.58}\)
\(A=\dfrac{2.3.4.5.6....56.57}{1.2.3.4.5.....57.58}=\dfrac{1}{58}\)
\(B=\left(81-\dfrac{3}{4}\right)\left(81-\dfrac{3^2}{5}\right).....\left(81-\dfrac{3^{2014}}{2017}\right)\)
Vì trong dãy số trên có một thừa số là \(\left(81-\dfrac{3^6}{9}\right)=\left(81-81\right)=0\)
\(\Rightarrow B=0\)
Vì \(a=A+B\Rightarrow a=\dfrac{1}{58}+0=\dfrac{1}{58}\)(1)
Thay (1) vào đa thức \(f\left(x\right)=5x-29a\) ta được:
\(f\left(x\right)=5x-29.\dfrac{1}{58}=5x-\dfrac{1}{2}\)
Ta lại có:
\(f\left(x\right)=0\Leftrightarrow5x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{10}\)
Vậy nghiệm của đa thức trên là \(\dfrac{1}{10}\)
Chúc bạn học tốt!!!
a: \(\dfrac{31995-81}{42660-108}=\dfrac{31914}{42552}=\dfrac{3}{4}\)
b: \(\dfrac{3\cdot5\cdot7\cdot11\cdot13\cdot37-10101}{1212120+40404}=\dfrac{545454}{1252524}=\dfrac{27}{62}\)
a, 31995−8142660−10831995−8142660−108
= 395.81−81395.108−108395.81−81395.108−108
=81.394394.10881.394394.108
= 8110881108 = 3434
b, 3.5.7.11.13.37−101011212120+404043.5.7.11.13.37−101011212120+40404
= 3.5.7.11.13.37−3.7.13.373.7.12.13.37.10+3.4.7.13.373.5.7.11.13.37−3.7.13.373.7.12.13.37.10+3.4.7.13.37
= (3.7.13.37)(5.11−1)(3.7.13.37)(120+4)(3.7.13.37)(5.11−1)(3.7.13.37)(120+4)
= 5.11−1120+45.11−1120+4
= 5412454124 = 2762