Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ơ bạn :\(\dfrac{cos\left(x+y\right)+cosx}{cos\left(x+y\right)-cosx}=\dfrac{2cos\left(\dfrac{2x+y}{2}\right).cos\left(\dfrac{y}{2}\right)}{-2sin\left(\dfrac{2x+y}{2}\right).sin\left(\dfrac{y}{2}\right)}=-2.cot\left(\dfrac{2x+y}{2}\right).cot\left(\dfrac{y}{2}\right)\) L không thể bẳng 0 được

\(a,\left(\frac{tan^2x-1}{2tanx}\right)^2-\frac{1}{4sin^2x.cos^2x}=-1\)
\(VT=\left(\frac{tan^2x-1}{2tanx}\right)^2-\frac{1}{4.sin^2x.cos^2x}=\left(\frac{1}{tan2x}\right)^2-\frac{1}{sin^22x}=\left(\frac{cos2x}{sin2x}\right)^2-\frac{1}{sin^22x}=\frac{cos^22x-1}{sin^22x}=\frac{-sin^22x}{sin^22x}=-1=VP\)
b, \(VT=\frac{cos^2x-sin^2x}{sin^4x+cos^4x-sin^2x}=\frac{cos2x}{\left(sin^2x+cos^2x\right)^2-sin^2x-2.sin^2x.cos^2x}=\frac{cos2x}{1-sin^2x-2.sin^2x.cos^2x}=\frac{cos2x}{cos^2x-2.sin^2x.cos^2x}\)
=\(\frac{cos2x}{cos^2x.\left(1-2.sin^2x\right)}=\frac{cos2x}{cos^2x.cos2x}=\frac{1}{cos^2x}=1+tan^2x=VP\)
d, \(VT=\left(\frac{cosx}{1+sinx}+tanx\right).\left(\frac{sinx}{1+cosx}+cotx\right)=\left(\frac{cosx}{1+sinx}+\frac{sinx}{cosx}\right).\left(\frac{sinx}{1+cosx}+\frac{cosx}{sinx}\right)\)
\(=\left(\frac{cos^2x+sinx.\left(1+sinx\right)}{cosx.\left(1+sinx\right)}\right).\left(\frac{sin^2x+cosx.\left(1+cosx\right)}{sinx.\left(1+cosx\right)}\right)=\left(\frac{cos^2x+sinx+sin^2x}{cosx.\left(1+sinx\right)}\right).\left(\frac{sin^2x+cosx+cos^2x}{sinx.\left(1+cosx\right)}\right)\)
=\(\frac{1}{cosx.sinx}=VP\)
e, \(VT=cos^2x.\left(cos^2x+2sin^2x+sin^2x.tan^2x\right)=cos^2x.\left(1+sin^2x.\left(1+tan^2x\right)\right)=cos^2x.\left(1+tan^2x\right)=cos^2x.\frac{1}{cos^2x}=1=VP\)
c, \(VT=\frac{sin^2x}{cosx.\left(1+tanx\right)}-\frac{cos^2x}{sinx.\left(1+cosx\right)}=\frac{sin^3x.\left(1+cosx\right)-cos^3x.\left(1+tanx\right)}{sinx.cosx.\left(1+tanx\right).\left(1+cosx\right)}\)
=\(\frac{sin^3x+sin^3x.cotx-cos^3x-cos^3.tanx}{\left(sinx+cosx\right)^2}=\frac{sin^3x+sin^2xcosx-cos^3x-cos^2sinx}{\left(sinx+cosx\right)^2}=\frac{sin^2x.\left(sinx+cosx\right)-cos^2x.\left(sinx+cosx\right)}{\left(sinx+cosx\right)^2}\)
\(=\frac{\left(sin^2x-cos^2x\right).\left(sinx+cosx\right)}{\left(sinx+cosx\right)^2}=\frac{\left(sinx-cosx\right).\left(sinx+cosx\right).\left(sinx+cosx\right)}{\left(sinx+cosx\right)^2}=sinx-cosx=VP\)
Đây nha bạn

Biến đổi pt trên như sau:
sinx.cosx/4 + cosx.sinx/4 - 3(sin2x + cos2x) + cosx = 0
sin(x + x/4) + cosx = 3
sin5x/4 + cosx = 3
Vì sin5x/4 \(\le\) 1 và cosx \(\le\) 1. Do đó sin5x/4 + cosx \(\le\) 2. Vì vậy pt trên vô nghiệm.

đề bài đầy đủ: rút gọn các biểu thức lượng giác sau trên điều kiện xác định của chúng:
\(\frac{sin^2x}{cosx+cosx.\frac{sinx}{cosx}}-\frac{cos^2x}{sinx+sinx.\frac{cosx}{sinx}}=\frac{sin^2x}{sinx+cosx}-\frac{cos^2x}{sinx+cosx}=\frac{sin^2x-cos^2x}{sinx+cosx}\)
\(=\frac{\left(sinx+cosx\right)\left(sinx-cosx\right)}{sinx+cosx}=sinx-cosx\)
\(\left(\frac{sinx}{cosx}+\frac{cosx}{1+sinx}\right)\left(\frac{cosx}{sinx}+\frac{sinx}{1+cosx}\right)=\left(\frac{sinx+sin^2x+cos^2x}{cosx\left(1+sinx\right)}\right)\left(\frac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}\right)\)
\(=\left(\frac{sinx+1}{cosx\left(1+sinx\right)}\right)\left(\frac{cosx+1}{sinx\left(1+cosx\right)}\right)=\frac{1}{sinx.cosx}\)

\(\frac{sin^2x+cos^2x+2sinx.cosx}{sinx+cosx}-\left(1-tan^2\frac{x}{2}\right).cos^2\frac{x}{2}\)
\(=\frac{\left(sinx+cosx\right)^2}{sinx+cosx}-\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)\)
\(=sinx+cosx-cosx=sinx\)
\(sin^4x+cos^4\left(x+\frac{\pi}{4}\right)=\left(\frac{1}{2}-\frac{1}{2}cos2x\right)^2+\left(\frac{1}{2}+\frac{1}{2}cos\left(2x+\frac{\pi}{2}\right)\right)^2\)
\(=\frac{1}{4}-\frac{1}{2}cos2x+\frac{1}{4}cos^22x+\left(\frac{1}{2}-\frac{1}{2}sin2x\right)^2\)
\(=\frac{1}{4}-\frac{1}{2}cos2x+\frac{1}{4}cos^22x+\frac{1}{4}-\frac{1}{2}sin2x+\frac{1}{4}sin^22x\)
\(=\frac{1}{4}-\frac{1}{2}\left(cos2x+sin2x\right)+\frac{1}{4}\left(cos^22x+sin^22x\right)\)
\(=\frac{3}{4}-\frac{\sqrt{2}}{2}sin\left(2x+\frac{\pi}{4}\right)\)

\(A=\frac{2sinx.cosx+sinx}{1+2cos^2x-1+cosx}=\frac{sinx\left(2cosx+1\right)}{cosx\left(2cosx+1\right)}=\frac{sinx}{cosx}=tanx\)
\(B=\frac{cosa}{sina}\left(\frac{1+sin^2a}{cosa}-cosa\right)=\frac{cosa}{sina}\left(\frac{1+sin^2a-cos^2a}{cosa}\right)=\frac{cosa}{sina}.\frac{2sin^2a}{cosa}=2sina\)
\(C=\frac{1+cos2x+cosx+cos3x}{2cos^2x-1+cosx}=\frac{1+2cos^2x-1+2cos2x.cosx}{cos2x+cosx}=\frac{2cosx\left(cosx+cos2x\right)}{cos2x+cosx}=2cosx\)
\(D=\frac{2sinx.cosx.\left(-tanx\right)}{-tanx.sinx}-2cosx=2cosx-2cosx=0\)
\(E=cos^2x.cot^2x-cot^2x+cos^2x+2cos^2x+2sin^2x\)
\(E=cot^2x\left(cos^2x-1\right)+cos^2x+2=\frac{cos^2x}{sin^2x}\left(-sin^2x\right)+cos^2x+2=2\)
\(F=\frac{sin^2x\left(1+tan^2x\right)}{cos^2x\left(1+tan^2x\right)}=\frac{sin^2x}{cos^2x}=tan^2x\)
Câu G mẫu số có gì đó sai sai, sao lại là \(2sina-sina?\)
\(H=sin^4\left(\frac{\pi}{2}+a\right)-cos^4\left(\frac{3\pi}{2}-a\right)+1=cos^4a-sin^4a+1\)
\(=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)+1=cos^2a-\left(1-cos^2a\right)+1=2cos^2a\)

\(cot^2x-cos^2x=\frac{cos^2x}{sin^2x}-cos^2x=cos^2x\left(\frac{1}{sin^2x}-1\right)=\frac{cos^2x\left(1-sin^2x\right)}{sin^2x}\)
\(=cos^2x.\left(\frac{cos^2x}{sin^2x}\right)=cot^2x.cos^2x\)
\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{\left(cosx-sinx\right)\left(cosx+sinx\right)}\)
\(=\frac{cos^2x+sin^2x+2sinx.cosx-\left(cos^2x+sin^2x-2sinx.cosx\right)}{cos^2x-sin^2x}=\frac{4sinx.cosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)
\(\frac{sin4x+cos2x}{1-cos4x+sin2x}=\frac{2sin2x.cos2x+cos2x}{1-\left(1-2sin^22x\right)+sin2x}=\frac{cos2x\left(2sin2x+1\right)}{sin2x\left(2sin2x+1\right)}=\frac{cos2x}{sin2x}=cot2x\)
\(A=sin^2x\left(sinx+cosx\right)+cos^2x\left(sinx+cosx\right)\)
\(=\left(sin^2x+cos^2x\right)\left(sinx+cosx\right)=sinx+cosx\)
\(B=\frac{sinx}{cosx}\left(\frac{1+cos^2x-sin^2x}{sinx}\right)=\frac{sinx}{cosx}\left(\frac{2cos^2x}{sinx}\right)=2cosx\)

\(2sin\left(\frac{\pi}{2}+x\right)+sin\left(3\pi-x\right)+sin\left(\frac{3\pi}{2}+x\right)+cos\left(\frac{\pi}{2}+x\right)\)
\(=2cosx+sinx-cosx-sinx\)
\(=cosx\)

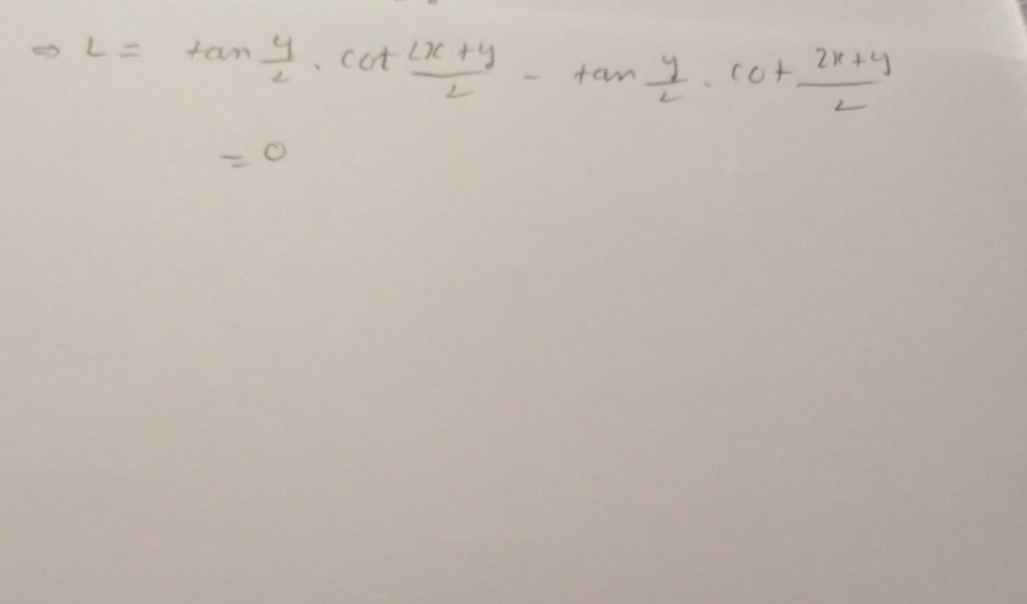
Lời giải:
$A=\frac{2\cos \frac{2x+y}{2}\sin \frac{x}{2}}{2\sin \frac{2x+y}{2}.\cos \frac{x}{2}}-\frac{2\cos \frac{2x+y}{2}\cos \frac{x}{2}}{-2\sin \frac{2x+y}{2}\sin \frac{x}{2}}$
$=\tan \frac{x}{2}.\cot \frac{2x+y}{2}+\cot \frac{x}{2}.\cot \frac{2x+y}{2}=\cot \frac{2x+y}{2}(\tan \frac{x}{2}+\cot \frac{x}{2})$
thank you so much