Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
\(=\sqrt{4.5}-\sqrt{9.5}+3\sqrt{18}+\sqrt{4.18}\)
\(=2\sqrt{5}-3\sqrt{5}+3\sqrt{18}+2\sqrt{18}\)
\(=-\sqrt{5}+5\sqrt{18}\)

a, \(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\sqrt{20}+\sqrt{5}\)
\(=\sqrt{5}+\dfrac{1}{2}.2\sqrt{5}+\sqrt{5}\)
\(=3\sqrt{5}\)
b, \(\sqrt{\dfrac{1}{2}}+\sqrt{4,5}+\sqrt{12,5}\)
\(=\sqrt{0,5}+3\sqrt{0,5}+5\sqrt{0,5}=9\sqrt{0,5}\)
c, \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
\(=2\sqrt{5}-3\sqrt{5}+3\sqrt{18}+2\sqrt{18}\)
\(=-\sqrt{5}+5\sqrt{18}\)
d, \(0,1.\sqrt{200}+2\sqrt{0,08}+0,4\sqrt{50}\)
\(=\sqrt{0,01.200}+0,2.\sqrt{2}+0,4.5\sqrt{2}\)
\(=\sqrt{2}+0,2\sqrt{2}+2\sqrt{2}=3,2\sqrt{2}\)
Chúc bạn học tốt!!!

\(B=\frac{9\sqrt{5}+3\sqrt{27}}{\sqrt{5}+\sqrt{3}}=\frac{9\sqrt{5}+9\sqrt{3}}{\sqrt{5}+\sqrt{3}}=\frac{9\left(\sqrt{5}+\sqrt{3}\right)}{\sqrt{5}+\sqrt{3}}=9\)
\(C=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{4}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)+\sqrt{2}.\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)\left(\sqrt{2}+1\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\sqrt{2}+1\)
mik chỉnh lại đề
\(D=\frac{3\sqrt{8}-2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}=\frac{6\sqrt{2}-4\sqrt{3}+2\sqrt{5}}{9\sqrt{2}-6\sqrt{3}+3\sqrt{5}}\)
\(=\frac{2\left(3\sqrt{2}-2\sqrt{3}+\sqrt{5}\right)}{3\left(3\sqrt{2}-2\sqrt{3}+\sqrt{5}\right)}=\frac{2}{3}\)

a: \(=10\sqrt{2}-4\sqrt{2}+6\sqrt{2}=12\sqrt{2}\)
b: \(=5\sqrt{7}-4\sqrt{7}+3\sqrt{7}=4\sqrt{7}\)
c: \(=\dfrac{3}{2}\sqrt{6}+\dfrac{2}{3}\sqrt{6}-2\sqrt{6}=\dfrac{1}{6}\sqrt{6}\)
d: \(=8\sqrt{5}-15\sqrt{5}+15\sqrt{5}-3\sqrt{5}=5\sqrt{5}\)
e: \(=\sqrt{5}+\dfrac{2}{5}\sqrt{5}+\sqrt{5}=2.4\sqrt{5}\)
f: \(=\dfrac{1}{5}\sqrt{5}+\dfrac{3}{2}\sqrt{2}+\dfrac{5}{2}\sqrt{2}=\dfrac{1}{5}\sqrt{5}+4\sqrt{2}\)

TRẢ LỜI :
\(=\sqrt{5}+\sqrt{5}+\sqrt{5}=3\sqrt{5}\)
c) √20 - √45 + 3√18 + √72
= √4.5 - √9.5 + 3√9.2 + √36.2
= 2√5 - 3√5 + 9√2 + 6√2
= -√5 + 15√2
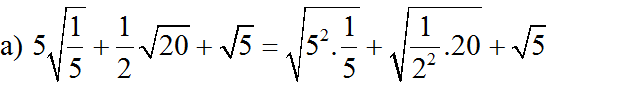

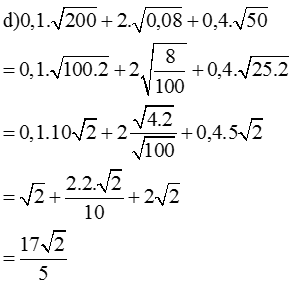
a) \(\sqrt{\frac{1}{2}}+\sqrt{4,5}+\sqrt{12,5}=\sqrt{\frac{1}{2}}+\sqrt{\frac{9}{2}}+\sqrt{\frac{25}{2}}=\sqrt{\frac{1}{2}}+3\sqrt{\frac{1}{2}}+5\sqrt{\frac{1}{2}}=9\sqrt{\frac{1}{2}}\)
b) \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}=\sqrt{4.5}-\sqrt{9.5}+3\sqrt{9.2}+\sqrt{36.2}=2\sqrt{5}-3\sqrt{5}+9\sqrt{2}+6\sqrt{2}=-\sqrt{5}+15\sqrt{2}\)
a) \(\sqrt{\frac{1}{2}}+\sqrt{4,5}+\sqrt{12,5}=\frac{\sqrt{2}}{2}+\frac{3\sqrt{2}}{2}+\frac{5\sqrt{2}}{2}=\frac{9\sqrt{2}}{2}\)
b) \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}=2\sqrt{5}-3\sqrt{5}+9\sqrt{2}+6\sqrt{2}=-\sqrt{5}+15\sqrt{2}=15\sqrt{2}-\sqrt{5}\)