K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 4 2021
\(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}-\frac{3-\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{3+\sqrt{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)
23 tháng 4 2021
a, \(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt[]{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)
AH
Akai Haruma
Giáo viên
29 tháng 12 2023
Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ bạn tốt hơn nhé.
HL
1
4 tháng 12 2021
\(a,ĐK:x>0;x\ne1;x\ne4\\ b,P=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1-x+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\\ P=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{3}=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
10 tháng 11 2021
\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện
12 tháng 4 2022
\(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{x-9}\)
\(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{x+3\sqrt{x}+\sqrt{x}+3+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{x+15\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(P=A+B=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{x+15\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+x+15\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{2x-6\sqrt{x}+x+15\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{3\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)
NV
1
LT
7 tháng 6 2021
ĐK: \(\left\{{}\begin{matrix}x-2\sqrt{x}-3\ne0\\\sqrt{x}+1\ne0\\3-\sqrt{x}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)\ne0\\\sqrt{x}+1\ne0\left(hiển-nhiên\right)\\x\ne\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow x\ne\sqrt{3}\)
\(P=\dfrac{x\sqrt{x}-3}{x-2\sqrt[]{x}-3}-\dfrac{2\left(\sqrt{x-3}\right)}{\sqrt{x}+1}+\dfrac{\sqrt{x}+3}{3-\sqrt{x}}\)
\(\Leftrightarrow\dfrac{x\sqrt{x}-3}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}-\dfrac{2\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(-\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\)
\(\Leftrightarrow\dfrac{x\sqrt{x}-3-2\left(x-9\right)-x-\sqrt{x}-3\sqrt{x}-3}{\left(\sqrt{x+1}\right)\left(\sqrt{x}-3\right)}\)
\(\Leftrightarrow\dfrac{\left(x-4\right)\sqrt{x}-3x+12}{\left(\sqrt{x+1}\right)\left(\sqrt{x}-3\right)}\)
Chúc bạn học tốt ^^
LT
7 tháng 6 2021
Không thấy câu b =))
\(x=14-6\sqrt{5}=\left(3+\sqrt{5}\right)^2\)
\(\Rightarrow\sqrt{x}=3+\sqrt{5}\)
Thay vào ta được
\(\dfrac{14-6\sqrt{5}-3\left(14-6\sqrt{5}\right)+12}{\left(3+\sqrt{5}+1\right)\left(3+\sqrt{5}-3\right)}\)
\(=\dfrac{12\sqrt{5}-16}{\left(4+\sqrt{5}\right)\sqrt{5}}=\dfrac{12\sqrt{5}-16}{4\sqrt{5}+5}\)
TH
0
9 tháng 7 2018
\(\left(\sqrt{2}-3\right)^2+\sqrt{24}=\)\(\left(\sqrt{2}\right)^2-2.\sqrt{2}.\sqrt{3}+\left(\sqrt{3}\right)^2+\sqrt{24}\)
\(=2-2\sqrt{6}+3+\sqrt{24}\)
\(=5-2\sqrt{6}+\sqrt{4.6}\)
\(=5-2\sqrt{6}+\sqrt{4}.\sqrt{6}\)
\(=5-2\sqrt{6}+2\sqrt{6}\)
\(=5\)
Nhớ li ke mk nha !!!
9 tháng 7 2018
\(\left(\sqrt{2}-\sqrt{3}\right)^2+\sqrt{24}=\left(\sqrt{2}\right)^2-2.\sqrt{2}.\sqrt{3}+\left(\sqrt{3}\right)^2+\sqrt{24}\)
\(=2-2.\sqrt{6}+3+\sqrt{24}\)
\(=5-2\sqrt{6}+\sqrt{4.6}\)
\(=5-2\sqrt{6}+\sqrt{4}.\sqrt{6}\)
\(=5-2\sqrt{6}+2\sqrt{6}\)
\(=5\)
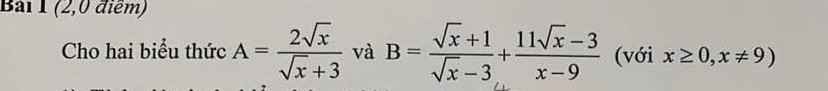
đk: \(-3\le x< 3\)
Ta có:
\(A=\frac{x^2+5x+x\sqrt{9-x^2}+6}{3x-x^2+\left(x+2\right)\sqrt{9-x^2}}=\frac{\left(x^2+5x+6\right)+x\sqrt{9-x^2}}{3x-x^2+\left(x+2\right)\sqrt{9-x^2}}\)
\(=\frac{\left(x+2\right)\left(x+3\right)+x\sqrt{\left(3-x\right)\left(x+3\right)}}{x\left(3-x\right)+\left(x+2\right)\sqrt{\left(3-x\right)\left(3+x\right)}}\)
\(=\frac{\left[\left(x+2\right)\sqrt{x+3}+x\sqrt{3-x}\right]\sqrt{x+3}}{\left(x\sqrt{3-x}+\left(x+2\right)\sqrt{3+x}\right)\sqrt{3-x}}\)
\(=\frac{\sqrt{x+3}}{\sqrt{3-x}}\)
t post lại lên thôi Dung nhá :))