
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

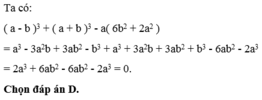

a) \(\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^{16}-1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^{32}-1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^{64}-1\right)\)
\(=\dfrac{3^{64}-1}{2}\)
b) \(\left(a+b+c\right)2+\left(a-b-c\right)2+\left(b-c-a\right)2+\left(c-a-b\right)2\)
\(=2\left[\left(a+b+c\right)+\left(a-b-c\right)+\left(b-c-a\right)+\left(c-a-b\right)\right]\)
\(=2\left(a+b+c+a-b-c+b-c-a+c-a-b\right)\)
\(=2.0\)
\(=0\)
c)\(\left(a+b+c+d\right)2+\left(a+b-c-d\right)2+\left(a+c-b-d\right)2+\left(a+d-b-c\right)2\)
\(=2\left(a+b+c+d+a+b-c-d+a+c-b-d+a+d-b-c\right)\)
\(=2.4a\)
\(=8a\)

Ta có :
\(M=a^3+b^3+c\left(a^2+b^2\right)-abc\)
\(M=a^3+b^3+a^2c+b^2c-abc\)
\(=\left(a^3+a^2c\right)+\left(b^3+b^2c\right)-abc\)
\(=a^2\left(a+c\right)+b^2\left(b+c\right)-abc\)
\(=a^2\left(-b\right)+b^2\left(-a\right)-abc\)
\(=-ab\left(a+b+c\right)=0\)
Ta có: \(a+b+c=0\)
\(\Rightarrow a+b=-c;b+c=-a;a+c=-b\)
\(M=a^3+b^3+c.\left(a^2+b^2\right)-abc\)
\(M=a^3+b^3+ca^2+cb^2-abc\)
\(M=a^2.\left(a+c\right)+b^2.\left(b+c\right)-abc\)
\(M=a^2.\left(-b\right)+b^2.\left(-a\right)\)
\(M=-a^2b-b^2a\)
\(M=-ab.\left(a+b\right)\)
\(M=-ab.\left(-c\right)\)
\(M=abc\)
Tham khảo nhé~

a, Gợi ý nà :3
a^2 + b^2 - c^2 +2ab = (a^2 + b^2 + 2ab) -c^2 = (a+b)^2 - c^2 = (a + b - c)(a + b + c)
a^2 - b^2 + c^2 + 2ac = (a + c)^2 - b^2 = (a + b + c)(a - b + c)
b. Gợi ý tiếp luôn nà :3
a^3 + b^3 + c^3 - 3abc
= (a^3 + b^3 +3a^2 x b + 3ab^2) - 3ab(a+b) -3abc + c^3
= (a+b)^3 + c^3 - 3ab(a+b+c)
= (a + b+ c)[(a+b)^2 - c(a+b) +c^2] - 3ab(a+b+c)
=(a+b+c)(a^2 + b^2 + c^2 -ac -bc + 2ab -3ab)
=(a+b+c)(a^2 + b^2 + c^2 - ab - bc -ca)
Rồi cứ thế rút gọn...
Học tốt nha bạn :3
\(\frac{a^2+2ab+b^2-c^2}{a^2+2ac+c^2-b^2}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+b+c\right)\left(a-b+c\right)}=\frac{a+b-c}{a-b+c}\)
\(\text{nhận xét: ta có hằng đẳng thức:}\)
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
đó đến đây bạn làm tiếp


Bài 1:
Từ \(a+b+c=0\) ta có:
\(B=\frac{a^2}{a^2-b^2-c^2}+\frac{b^2}{b^2-c^2-a^2}+\frac{c^2}{c^2-b^2-a^2}\)
\(=\frac{a^2}{(-b-c)^2-b^2-c^2}+\frac{b^2}{(-c-a)^2-c^2-a^2}+\frac{c^2}{(-b-a)^2-b^2-a^2}\)
\(=\frac{a^2}{2bc}+\frac{b^2}{2ac}+\frac{c^2}{2ab}=\frac{a^3+b^3+c^3}{2abc}\)
Lại có:
\(a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3=(-c)^3-3ab(-c)+c^3\)
\(=-c^3+3abc+c^3=3abc\)
Do đó \(B=\frac{3abc}{2abc}=\frac{3}{2}\)
Bài 2:
Lấy P-Q ta có:
\(P-Q=\left(\frac{a^3}{a^2+ab+b^2}+\frac{b^3}{b^2+bc+c^2}+\frac{c^3}{c^2+ca+a^2}\right)-\left(\frac{b^3}{a^2+ab+b^2}+\frac{c^3}{b^2+bc+c^2}+\frac{a^3}{c^2+ca+a^2}\right)\)
\(P-Q=\frac{a^3-b^3}{a^2+ab+b^2}+\frac{b^3-c^3}{b^2+bc+c^2}+\frac{c^3-a^3}{c^2+ac+a^2}\)
\(P-Q=\frac{(a-b)(a^2+ab+b^2)}{a^2+ab+b^2}+\frac{(b-c)(b^2+bc+c^2)}{b^2+bc+c^2}+\frac{(c-a)(c^2+ac+a^2)}{c^2+ac+a^2}\)
\(P-Q=(a-b)+(b-c)+(c-a)=0\Rightarrow P=Q\)
Ta có đpcm.

a^3+b^3+c^3-3abc
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab)...
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)
thay vào và rút gọn ta được:\(a+b+c\)

\(1,\frac{x^6+2x^3y^3+y^6}{x^7-xy^6}=\frac{\left(x^3+y^3\right)^2}{x\left(x^6-y^6\right)}=\frac{\left(x^3+y^3\right)^2}{x\left(x^3-y^3\right)\left(x^3+y^3\right)}=\frac{x^3+y^3}{x\left(x^3-y^3\right)}\)
\(2,=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+b+c\right)\left(a+c-b\right)}=\frac{a+b-c}{a+c-b}\)
pt thành nhân tử là ra

a, Điều kiện xác định: x<>0
b, Điều kiện xác định: x <> -1/3
c, Điều kiện xác định: x<>2
d, Điều kiện xác định: a<>0 và b<>0; b<>2a
A : không rút gọn được
\(B=\frac{4x^2\left(x-2\right)+3\left(x-2\right)}{3x\left(4x^2+3\right)+4x^2+3}=\frac{\left(4x^2+3\right)\left(x-2\right)}{\left(4x^2+3\right)\left(3x+1\right)}=\frac{x-2}{3x+1}\)
\(C=\frac{x^4-1}{x^3+2x^2-x-2}=\frac{\left(x^2-1\right)\left(x^2+1\right)}{\left(x+2\right)\left(x^2-1\right)}=\frac{x^2+1}{x+2}\)
\(D=\frac{a^3+b^3}{a^3+\left(a-b\right)^3}=\frac{\left(a+b\right)\left(a^2-ab+b^2\right)}{\left(a+a-b\right)\left(a^2-a^2+ab+a^2-2ab+b^2\right)}\)\(=\frac{\left(a+b\right)\left(a^2-ab+b^2\right)}{\left(2a-b\right)\left(a^2-ab+b^2\right)}=\frac{a+b}{2a-b}\)