Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: -8/31=-808/3131
-786/3131=-786/3131
b: \(\dfrac{11}{2^3\cdot3^4\cdot5^2}=\dfrac{11\cdot5}{2^3\cdot3^4\cdot5^3}=\dfrac{55}{2^3\cdot3^4\cdot5^3}\)
\(\dfrac{29}{2^2\cdot3^4\cdot5^3}=\dfrac{29\cdot2}{2^3\cdot3^4\cdot5^3}=\dfrac{58}{2^3\cdot3^4\cdot5^3}\)
c: 7/39=140/780
11/65=132/780
9/52=135/780

a: \(\dfrac{4\cdot5+4\cdot11}{8\cdot7+4\cdot3}=\dfrac{20+44}{56+12}=\dfrac{64}{68}=\dfrac{16}{17}=\dfrac{11088}{11781}\)
\(\dfrac{-15\cdot8+10\cdot7}{5\cdot6+20\cdot3}=\dfrac{-120+70}{30+60}=\dfrac{-50}{90}=\dfrac{-5}{9}=\dfrac{-6545}{11781}\)
\(\dfrac{2^4\cdot5^2\cdot7}{2^3\cdot5\cdot7^2\cdot11}=\dfrac{2\cdot5}{7\cdot11}=\dfrac{10}{77}=\dfrac{1530}{11781}\)

Câu 1:
\(\dfrac{14\cdot34-21\cdot10}{28\cdot10-28\cdot16}=\dfrac{7\cdot2\cdot34-7\cdot3\cdot10}{28\left(10-16\right)}\)
\(=\dfrac{7\left(2\cdot34-3\cdot10\right)}{28\cdot\left(-6\right)}=\dfrac{1}{4}\cdot\dfrac{68-30}{-6}=\dfrac{1}{4}\cdot\dfrac{38}{-6}=\dfrac{38}{-24}=-\dfrac{19}{12}\)

a: \(\dfrac{25\cdot9-25\cdot17}{-8\cdot80-8\cdot10}=\dfrac{25\cdot\left(-8\right)}{\left(-8\right)\cdot\left(80+10\right)}=\dfrac{25}{90}=\dfrac{5}{18}=\dfrac{250}{900}\)
\(\dfrac{48\cdot12-48\cdot15}{\left(-3\right)\cdot\left(270+30\right)}=\dfrac{48}{300}=\dfrac{8}{50}=\dfrac{144}{900}\)
\(\dfrac{2^5\cdot3}{600}=\dfrac{96}{600}=\dfrac{144}{900}\)
b: \(\dfrac{2^5\cdot7+25}{25\cdot5^2-2^5\cdot3}=\dfrac{32\cdot7+25}{25\cdot25-32\cdot3}=\dfrac{249}{529}=\dfrac{1743}{7\cdot529}\)
\(\dfrac{3^4\cdot5-3^6}{3^4\cdot13+3^4}=\dfrac{3^4\left(5-9\right)}{3^4\left(13+1\right)}=\dfrac{-4}{14}=\dfrac{-2}{7}=\dfrac{-1058}{7\cdot529}\)

Ta có: \(\dfrac{4.5^2}{5^3.6}=\dfrac{2.2.5^2}{5^2.5.2.3}=\dfrac{2}{15}\)
\(\dfrac{15}{1.2.3.4.5}=\dfrac{3.5}{1.2.3.4.5}=\dfrac{1}{8}\)
Quy đồng: \(\dfrac{2}{15}=\dfrac{16}{120}\) ; \(\dfrac{1}{8}=\dfrac{15}{120}\)
Vậy \(\dfrac{4.5^2}{5^3.6}=\dfrac{16}{120}\) và \(\dfrac{15}{1.2.3.4.5}=\dfrac{15}{120}\)

Đề bài :
a) dãy các phân số trên có phải theo quy luật ko ?
b) tính tổng các phân số của dãy trên
1) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{49.50}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(=1-\dfrac{1}{50}\)
\(=\dfrac{49}{50}\)
2) \(\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{37.39}\)
\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{37}-\dfrac{1}{39}\)
\(=\dfrac{1}{3}-\dfrac{1}{39}\)
\(=\dfrac{13}{39}-\dfrac{1}{39}=\dfrac{12}{39}=\dfrac{4}{13}\)
3) \(\dfrac{3}{4.7}+\dfrac{3}{7.10}+\dfrac{3}{10.13}+...+\dfrac{3}{73.76}\)
\(=\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{73}-\dfrac{1}{76}\)
\(=\dfrac{1}{4}-\dfrac{1}{76}\)
\(=\dfrac{19}{76}-\dfrac{1}{76}=\dfrac{18}{76}=\dfrac{9}{38}\)
1)
\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\\ =\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\\ =1-\dfrac{1}{50}\\ =\dfrac{49}{50}\)
2)
\(\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{37.39}\\ =\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{37}-\dfrac{1}{39}\\ =\dfrac{1}{3}-\dfrac{1}{39}\\ =\dfrac{13}{39}-\dfrac{1}{39}\\ =\dfrac{12}{39}=\dfrac{4}{13}\)
3) \(\dfrac{3}{4.7}+\dfrac{3}{7.10}+\dfrac{3}{10.13}+...+\dfrac{3}{73.76}\\ =\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{73}-\dfrac{1}{79}\\ =\dfrac{1}{4}-\dfrac{1}{79}\\ =\dfrac{75}{316}\)

\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{299}{600}\)
\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{299}{600}\)
\(\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{299}{600}\)
\(\dfrac{1}{x+1}=\dfrac{1}{2}-\dfrac{299}{600}\)
\(\dfrac{1}{x+1}=\dfrac{300}{600}-\dfrac{299}{600}\)
\(\dfrac{1}{x+1}=\dfrac{1}{600}\)
=> x + 1 = 600
x = 600 - 1
x = 599
Vậy x = 599
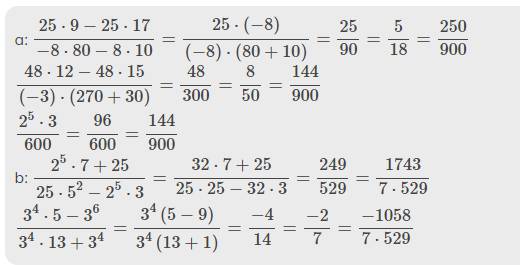
Ghi rõ đề ra chứ :((
Tớ ghi rõ rồi mà