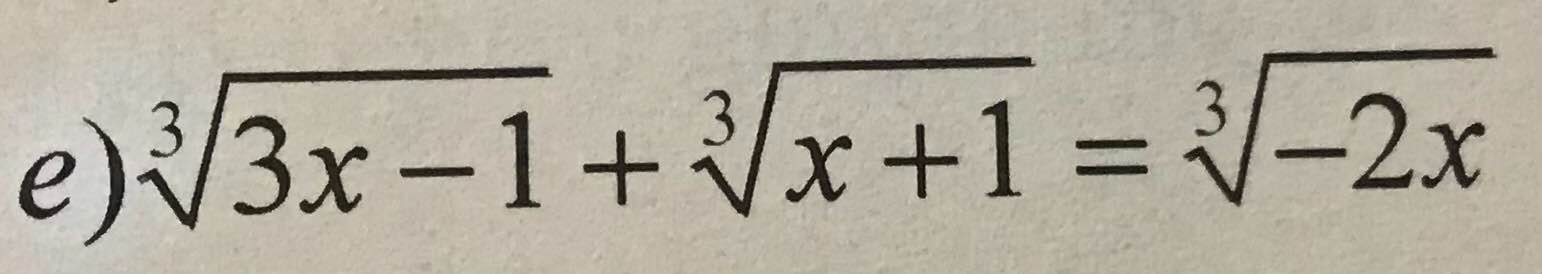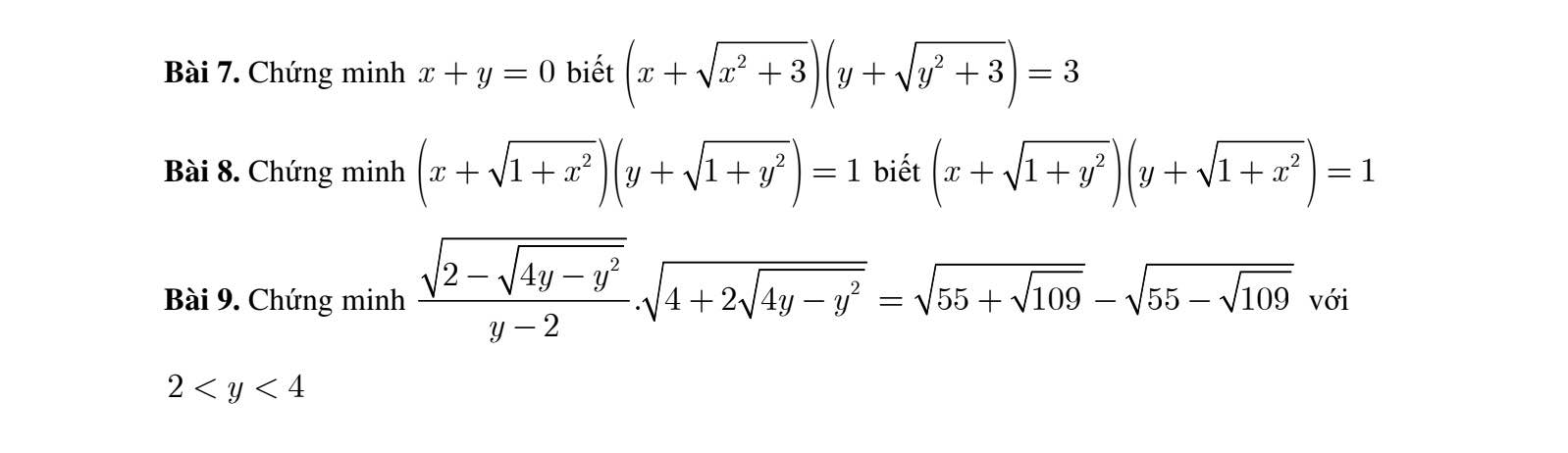Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt \(\left\{{}\begin{matrix}\sqrt[3]{3x-1}=a\\\sqrt[3]{x+1}=b\\\sqrt[3]{-2x}=c\end{matrix}\right.\) ta được hệ:
\(\left\{{}\begin{matrix}a+b=c\\a^3+b^3=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\\left(a+b\right)^3-3ab\left(a+b\right)=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c^3-3abc=-2c^3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left(c^2-ab\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+b\right)^2-ab\right]=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=c\\c\left[\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\right]=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=0\\a=b=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt[3]{-2x}=0\Leftrightarrow x=0\)

a: Xét tứ giác MAOC có góc MAO+góc MCO=180 độ
nên MAOC là tứ giác nội tiếp
b: ΔOBC cân tại O
mà OK là trung tuyến
nên OK là đường phân giác và OK vuông góc với BC
Xét ΔOBN và ΔOCN có
OB=OC
góc BON=góc CON
ON chung
Do đó: ΔOBN=ΔOCN
=>NB=NC
=>NB^2=NC^2=NK*NO

36B
37C
38D
39B
40D
41A
42B
43B
44A
45B
46B
47A
48C
50B
51B
52B
53D
54C
55D
56C


7. Ta có: \(\left(x+\sqrt{x^2+3}\right)\left(\sqrt{x^2+3}-x\right)=x^2+3-x=3\)
\(\Rightarrow\sqrt{x^2+3}-x=y+\sqrt{y^2+3}\Rightarrow x+y=\sqrt{x^2+3}-\sqrt{y^2+3}\left(1\right)\)
Lại có \(\left(y+\sqrt{y^2+3}\right)\left(\sqrt{y^2+3}-y\right)=y^2+3-y=3\)
\(\Rightarrow\sqrt{x^2+3}+x=\sqrt{y^2+3}-y\Rightarrow x+y=\sqrt{y^2+3}-\sqrt{x^2+3}\left(2\right)\)
Lấy \(\left(1\right)+\left(2\right)\Rightarrow2\left(x+y\right)=0\Rightarrow x+y=0\)
9. Ta có: \(\sqrt{55+\sqrt{109}}-\sqrt{55-\sqrt{109}}\)
\(=\sqrt{\dfrac{110+2\sqrt{109}}{2}}-\sqrt{\dfrac{110-2\sqrt{109}}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{109}+1\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{109}-1\right)^2}{2}}=\dfrac{\sqrt{109}+1}{\sqrt{2}}-\dfrac{\sqrt{109}-1}{\sqrt{2}}\)
\(=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
Lại có: \(\dfrac{\sqrt{2-\sqrt{4y-y^2}}}{y-2}.\sqrt{4+2\sqrt{4y-y^2}}\)
\(=\dfrac{\sqrt{4-2\sqrt{y\left(4-y\right)}}}{\sqrt{2}\left(y-2\right)}.\sqrt{\left(\sqrt{y}\right)^2+2\sqrt{y\left(4-y\right)}+\left(\sqrt{4-y}\right)^2}\)
\(\dfrac{\sqrt{\left(\sqrt{y}\right)^2-2\sqrt{y\left(4-y\right)}+\left(\sqrt{4-y}\right)^2}}{\sqrt{2}\left(y-2\right)}.\sqrt{\left(\sqrt{y}+\sqrt{4-y}\right)^2}\)
\(=\dfrac{\sqrt{\left(\sqrt{y}-\sqrt{4-y}\right)^2}}{\sqrt{2}\left(y-2\right)}.\left|\sqrt{y}+\sqrt{4-y}\right|=\dfrac{\left|\sqrt{y}-\sqrt{4-y}\right|}{\sqrt{2}\left(y-2\right)}.\left|\sqrt{y}+\sqrt{4-y}\right|\)
Vì \(y>2\Rightarrow\left\{{}\begin{matrix}\sqrt{y}>\sqrt{2}\\\sqrt{4-y}< \sqrt{2}\end{matrix}\right.\Rightarrow\sqrt{y}-\sqrt{4-y}>0\)
\(\Rightarrow\dfrac{\left|\sqrt{y}-\sqrt{4-y}\right|}{\sqrt{2}\left(y-2\right)}.\left|\sqrt{y}+\sqrt{4-y}\right|=\dfrac{\left(\sqrt{y}-\sqrt{4-y}\right)\left(\sqrt{y}+\sqrt{4+y}\right)}{\sqrt{2}\left(y-2\right)}\)
\(=\dfrac{y-\left(4-y\right)}{\sqrt{2}\left(y-2\right)}=\dfrac{2y-4}{\sqrt{2}\left(y-2\right)}=\dfrac{2\left(y-2\right)}{\sqrt{2}\left(y-2\right)}=\sqrt{2}\)
\(\Rightarrow\dfrac{\sqrt{2-\sqrt{4y-y^2}}}{y-2}.\sqrt{4+2\sqrt{4y-y^2}}=\sqrt{55+\sqrt{109}}-\sqrt{55-\sqrt{109}}\)

a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3