
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(x^2-6x+m-2=0\)
\(\Rightarrow\Delta=6^2-4\left(m-2\right)\)
Để phương tình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow36-4m+8>0\Leftrightarrow44>4m\Leftrightarrow11>m\)
Câu D


Câu 1: Cho t=1 ta có \(\left\{{}\begin{matrix}x=1+1\\y=2-2.1\\z=3+1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\\z=4\end{matrix}\right.\)
Vậy điểm M là M(2,0,4). Khoanh B.
Câu 2: Ta có tọa độ điểm O thuộc (d) là: O(1,2,3)
Để (d') cũng là phương trình tham số của (d) thì (d') phải đi qua điểm O(1,2,3)
Quan sát đáp án ta thấy đáp án B đúng.

26.
a.
\(\left|2x-3\right|\le x+3\Leftrightarrow\left\{{}\begin{matrix}x+3\ge0\\\left(2x-3\right)^2\le\left(x+3\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\x^2-6x\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\0\le x\le6\end{matrix}\right.\)
\(\Rightarrow0\le x\le6\)
b.
\(\sqrt{x^2+x-6}\ge x+2\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2< 0\\x^2+x-6\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x+2\ge0\\x^2+x-6\ge\left(x+2\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< -2\\\left[{}\begin{matrix}x\ge2\\x\le-3\end{matrix}\right.\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge-2\\3x\le-10\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow x\le-3\)
27.
Áp dụng định lý hàm cosin cho tam giác ABC:
\(cosB=\dfrac{AB^2+BC^2-AC^2}{2AB.BC}=\dfrac{1}{2}\)
Áp dụng định lý hàm cosin cho tam giác ABM:
\(AM=\sqrt{AB^2+BM^2-2AB.BM.cosB}=\sqrt{31}\)

19.
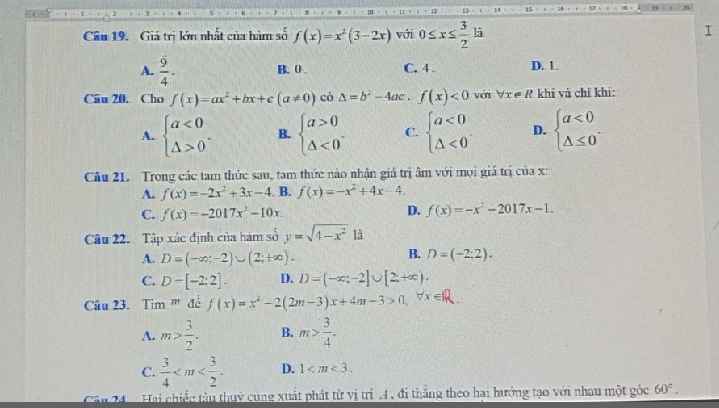
\(f\left(x\right)=x^2\left(3-2x\right)=x.x.\left(3-2x\right)\le\left(\dfrac{x+x+3-2x}{3}\right)^3=1\)
\(\Rightarrow\max\limits_{\left[0;\dfrac{3}{2}\right]}f\left(x\right)=1\)
20.
\(f\left(x\right)< 0;\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)
21.
A là đáp án đúng, do đa thức \(f\left(x\right)=-2x^2+3x-4\) có:
\(\left\{{}\begin{matrix}a=-2< 0\\\Delta=3^2-4.\left(-2\right).\left(-4\right)=-23< 0\end{matrix}\right.\)
22.
ĐKXĐ: \(4-x^2\le0\Rightarrow\left(2-x\right)\left(2+x\right)\le0\)
\(\Rightarrow-2\le x\le2\Rightarrow D=\left[-2;2\right]\)
23.
\(f\left(x\right)>0;\forall x\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(2m-3\right)^2-\left(4m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-16m+12< 0\)
\(\Rightarrow1< m< 3\)

Bài 1:
Do d đi qua A nên phương trình d có dạng:
\(a\left(x-2\right)+b\left(y-5\right)=0\Leftrightarrow ax+by-2a-5b=0\) (1) với \(a^2+b^2>0\)
Áp dụng công thức khoảng cách:
\(d\left(I;d\right)=\dfrac{\left|a.4+b.1-2a-5b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|2a-4b\right|=2\sqrt{a^2+b^2}\)
\(\Leftrightarrow\left|a-2b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow a^2-4ab+4b^2=a^2+b^2\)
\(\Leftrightarrow3b\left(3b-4a\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\b=\dfrac{4a}{3}\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow\left[{}\begin{matrix}ax+0.y-2a-5.0=0\\ax+\dfrac{4a}{3}.y-2a-5.\dfrac{4a}{3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\3x+4y-26=0\end{matrix}\right.\)
Bài 2:
Bài này có nhiều cách làm, (ví dụ viết phương trình đường thẳng d, tính khoảng cách tới A và B rồi cho chúng bằng nhau, từ đó suy ra tương tự câu a), hoặc đơn giản hơn là lý luận như sau:
Đường thẳng d cách đều 2 điểm AB khi nó thỏa mãn 1 trong 2 trường hợp sau:
TH1: d song song AB
Ta có \(\overrightarrow{AB}=\left(-2;8\right)=2\left(-1;4\right)\Rightarrow d\) nhận (4;1) là 1 vtpt (do d song song AB)
Phương trình d có dạng:
\(4\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow4x+y+5=0\)
TH2: d đi qua trung điểm của AB
Gọi M là trung điểm AB, theo công thức trung điểm ta có \(M\left(4;3\right)\Rightarrow\overrightarrow{IM}=\left(6;0\right)=6\left(1;0\right)\)
\(\Rightarrow\) Đường thẳng d (hay IM) nhận (0;1) là 1 vtpt
Phương trình: \(0\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow y-3=0\)

Câu 9: A
Câu 10: C
Câu 11: C
Câu 12: A
Câu 13; B
Câu 14: C








\(\frac{x-1}{x+1}\le0\Leftrightarrow-1< x\le1\Rightarrow S_1=(-1;1]\)
\(-2x+m>0\Leftrightarrow x< \frac{m}{2}\Rightarrow S_2=\left(-\infty;\frac{m}{2}\right)\)
\(S_1\subset S_2\Leftrightarrow\frac{m}{2}>1\Leftrightarrow m>2\)
Vì \(m\in Z;m\in\left[-10;10\right]\) nên \(m=\left\{3;4;5;...;10\right\}\)(8 giá trị)