Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔCAD và ΔCBD, ta có:
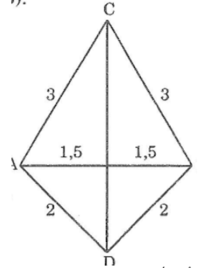
AC = BC (= 3 cm)
AD = BD (= 2 cm)
CD cạnh chung
Suy ra: ΔCAD= ΔCBD(c.c.c)
Vậy ∠(CAD) =∠(CBD) ̂(hai góc tương ứng)

Xét tam giác ABC và tam giác ABD, có:
AC=CD ( gt )
CD là cạnh chung
AD=BD ( gt )
Vậy CAD=CBD (c.c.c )


xét 2 tam giác ACD và BCD có AD=BD=2cm, AC=BC=3cm, CD chung
=> tg ACD= tg BCD (c.c.c) =>góc CAD= góc CBD

Trả lời :
A D C B
a , Xét tam giác ACD và tam giác CBD có :
AD = BD ( gt )
CD : Cạnh chung
AC = BC ( gt )
Vậy tam giác ACB = tam giác CBD ( c . c .c )
b ) Theo câu a, tam giác ACD = tam giác CBD
=> \(\widehat{CAB}\) \(=\) \(\widehat{CBD}\) ( góc tương ứng )
c , Cũng từ a , ta có : tam giác ACD = tam giác CBD
=> \(\widehat{ADC}\) \(=\) \(\widehat{BDC}\) ( góc tương ứng )
mà \(\widehat{ADC}\) \(+\) \(\widehat{BDC}\) \(=\) \(\widehat{ADB}\) nên => CD là tia phân giác của \(\widehat{ACD}\)
_Học tốt ạ :)
góc CAD = góc CBD