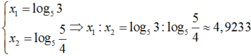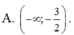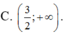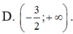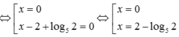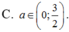Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x>0\)
\(x^{log_25}=t\Rightarrow25^{log_2x}=\left(5^{log_2x}\right)^2=\left(x^{log_25}\right)^2=t^2\)
\(x_1x_2=4\Rightarrow t_1t_2=\left(x_1x_2\right)^{log_25}=4^{log_25}=25\)
\(\left(m+1\right)t^2+\left(m-2\right)t-2m+1=0\) (1)
Pt có 2 nghiệm pb \(\Rightarrow\) (1) có 2 nghiệm dương pb
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-2\right)^2-4\left(m+1\right)\left(-2m+1\right)>0\\t_1+t_2=\dfrac{2-m}{m+1}>0\\t_1t_2=\dfrac{-2m+1}{m+1}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\-1< m< \dfrac{1}{2}\end{matrix}\right.\)
Ủa làm đến đây mới thấy kì kì, chỉ riêng hệ điều kiện này đã ko tồn tại m nguyên rồi, chưa cần điều kiện \(x_1x_2=4\)
cái này mk làm 1 nghiệm t =1 xong thay tìm m, có vẻ cũng ko dài lắm :))))

\(\left(5+\sqrt{24}\right)^{x^2-2x-2}=49-10\sqrt{24}\)
=>\(\left(5+\sqrt{24}\right)^{x^2-2x-2}=\left(5-\sqrt{24}\right)^2\)
=>\(\left(5+\sqrt{24}\right)^{x^2-2x-2}=\left(5+\sqrt{24}\right)^{-2}\)
=>\(x^2-2x-2=-2\)
=>\(x^2-2x=0\)
=>x(x-2)=0
=>x=0 hoặc x=2
=>x1-x2=0-2=-2

Chọn C.
Điều kiện: 5x – 1 > 0 hay x > 0
Phương trình đã cho tương đương:
log2( 5x - 1) [log2( 5x - 1) + 1] = 2
Đặt t = log2(5x - 1), khi đó phuơng trình trở thành: t(t + 1) = 2
Suy ra t = 1 hoặc t = -2
Với t =1 ta có log2(5x - 1) = 1 nên 5x – 1 = 2; x = log53
Với t = -2ta có log2(5x - 1) = - 2 nên 5x – 1 = 2-2; x = log5(5/4)
Mặt khác x1 > x2 suy ra