Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
1. hai tam giác bằng nhau là hai tam giác có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
2. tam giác ABC là tam giác đều(vẽ hình ,CM là ra)
3. trong 1 tam giác nếu bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại thì tamm giác đó là tam giác vuông.
4. tổng ba góc của 1 tam giác = 180độ , góc ngoài của tam giác = tổng 2 góc trong ko kề vs nó
5. TH1: nếu 3 cạnh của tam giác này lần lượt = 3 cạnh của tam giác kia thì 2 tam giác đó = nhau (c.c.c)
TH2 : nếu 2 cạnh và 1 óc xen giữa của tam giác này = 2 cạnh và góc xen giữa của tam giác kia thì 2 tam giác đó = nhau( c.g.c)
TH3: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau(g.c.g)
6.- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp c.g.c)
- Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (g.c.g).
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (g.c.g).
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
hok tốt

1)
Lý thuyết về hai góc đối đỉnh.
Kiến thức cơ bản:
1. Hai góc đối đỉnh:
Hai góc đối đỉnh là hai góc mà mối cạnh của góc này là tia đối của một cạnh của góc kia.
2. Tính chất:
Hai góc đối đỉnh thì bằng nhau
VD: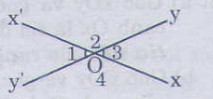
ˆO1O1^ đối đỉnh với ˆO3⇒ˆO1=ˆO3O3^⇒O1^=O3^
ˆO2O2^ đối đỉnh với ˆO4⇒ˆO2=ˆO4
ĐỊNH LÝ:
Hai góc đối đỉnh thì bằng nhau
Hai góc đối đỉnh là 2 góc có cạnh của góc này là tia đối của cạnh góc kia

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

Bài 1:
I. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh:
1) Vẽ tam giác biết độ dài 3 cạnh: (HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = 3cm, BC = 5cm, AC = 4cm.
2) Trường hợp bằng nhau cạnh – cạnh – cạnh:
“Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.”
II. Trường hợp bằng nhau thứ nhất của tam giác cạnh – góc – cạnh:
1) Vẽ tam giác biết độ dài 2 cạnh và 1 góc xen giữa:
(HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = BC = 4cm,
2) Trường hợp bằng nhau cạnh – góc – cạnh:
“Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.”
* Lưu ý: Cặp góc bằng nhau phải xen giữa hai cặp cạnh bằng nhau thì mới kết luận được hai tam giác bằng nhau.
III. Trường hợp bằng nhau thứ nhất của tam giác góc – cạnh – góc:
1) Vẽ tam giác biết độ dài 1 cạnh và 2 góc kề:
(HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AC = 5cm,
2) Trường hợp bằng nhau góc – cạnh – góc:
“Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.”
* Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
* Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề ấy cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g-c-g)
* Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (ch-gn)

b: Tính chất: góc ngoài của tam giác có số đo bằng tổng số đo hai góc trong không kề với nó

a) Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
b) Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
c) Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Có 4 trường hợp bằng nhau của tam giác vuông:
+) Hai tam giác vuông có hai cạnh góc vuông bằng nhau thì bằng nhau
+) Hai tam giác vuông có cạnh huyền và một góc nhọn bằng nhau thì bằng nhau
+) Hai tam giác vuông có một cạnh góc vuông và một góc nhọn kề cạnh ấy bằng nhau thì bằng nhau
+) Hai tam giác vuông có cạnh huyền và một cạnh góc vuông bằng nhau thì bằng nhau
1. Các trường hợp bằng nhau đã biết của hai tam giác vuông.
- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau(theo trường hợp c.g.c)
- Nếu một cạnh của tam giác vuông này và một góc nhọn kề cạnh ấy bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
2. Trường hợp bằng nhau về cạnh huyền mà một cạnh góc vuông
Nếu cạnh huyền và môt cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.