
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Định lí (trang 101 sgk Đại Số 10):
Cho tam thức f(x) = ax2 + bx + c (a ≠ 0), Δ = b2 – 4ac
- Nếu Δ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ R.
- Nếu Δ = 0 thì f(x) cùng dấu với hệ số a với mọi x ≠ -b/2a.
- Nếu Δ > 0 thì f(x) cùng dấu với hệ số a khi x < x1 hoặc x > x2
f(x) trái dấu với hệ số a khi x1 < x < x2 trong đó x1, x2 là hai nghiệm của f(x) và x1 < x2.

Cách nhận biết đa thức
\(f\left(x\right)=ax^2+bx+c\)
Có nghiệm hay vô nghiệm
Lập \(\Delta\) ( đọc là delta )
\(\Delta=b^2-4ac\)
Nếu \(\Delta< 0\) : đa thức vô nghiệm
Nếu \(\Delta\ge0\) : đa thức có nghiệm
Nếu \(\Delta>0\) : đa thức có hai nghiệm
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)

Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).

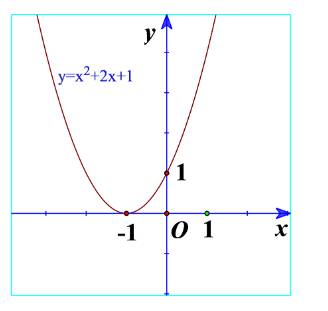
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)
Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
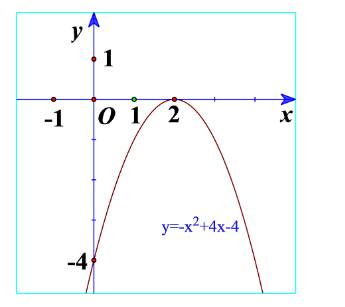
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)
Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)

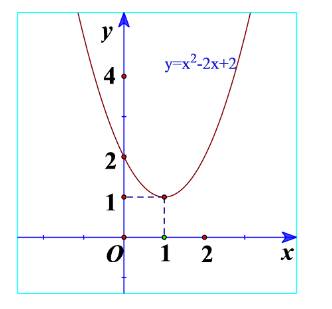
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
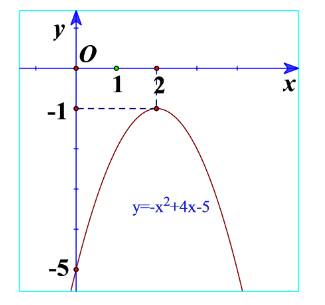
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.

Do b là cạnh của tam giác nên b > 0
Đặt \(f\left(x\right)=b^2x^2-\left(b^2+c^2-a^2\right)x+c^2>0,\forall x\)
Theo định lý của dấu về tam thức bậc 2
\(\Rightarrow\left\{{}\begin{matrix}b^2>0\left(đúng\right)\\\Delta< 0\end{matrix}\right.\)\(\Rightarrow\Delta< 0\)
\(\Leftrightarrow\Delta=\left(b^2+c^2-a^2\right)^2-4b^2c^2< 0\)
Chứng minh rằng \(\Delta=\left(b^2+c^2-a^2\right)^2-4b^2c^2< 0\)
\(\Leftrightarrow\left(b^2+c^2-a^2\right)^2< 4b^2c^2\)
\(\Leftrightarrow b^2+c^2-a^2< 2bc\)
\(\Leftrightarrow b^2-2bc+c^2< a^2\)
\(\Leftrightarrow\left(b-c\right)^2< a^2\)
\(\Leftrightarrow b-c< a\)
\(\Leftrightarrow b< c+a\)
Theo bất đẳng thức tam giác thì \(b< c+a\)
\(\Rightarrow\)\(\Delta=\left(b^2+c^2-a^2\right)^2-4b^2c^2< 0\) ( đpcm )
Vậy \(f\left(x\right)=b^2x^2-\left(b^2+c^2-a^2\right)x+c^2>0,\forall x\)

Các định lí trên có thể được phát biểu là:
a) Một phương trình bậc hai có biệt thức dương là điều kiện cần và đủ để có hai nghiệm phân biệt
b) Một hình bình hành có hai đường chéo vuông góc với nhau là điều kiện cần và đủ để nó là hình thoi.

P ⇒ Q: “ Nếu tam giác ABC có hai góc bằng 60o thì ABC là một tam giác đều”
Giả thiết: “Tam giác ABC có hai góc bằng 60o ”
Kết luận: “ABC là một tam giác đều”
Phát biểu lại định lí này dưới dạng điều kiện cần: “ABC là một tam giác đều là điều kiện cần để tam giác ABC có hai góc bằng 60o”
Phát biểu lại định lí này dưới dạng điều kiện đủ : “Tam giác ABC có hai góc bằng 60o là điều kiện đủ để ABC là tam giác đều”

a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai
\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)
b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai
c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai
\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)

Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x =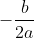 , với mọi x ≠
, với mọi x ≠ 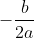 , f(x) có cùng dấu với hệ số a.
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).