Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khi a = 2, ta có hệ phương trình
![]()
![]()
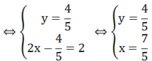
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7/5; 4/5)

a) x 2 - 7x + 5 = 0
Δ = 7 2 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
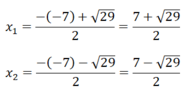
Vậy hệ phương trình đã cho có tập nghiệm
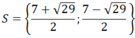

x - 3 2 + x + 4 2 = 23 - 3x
⇔ x 2 - 6x + 9 + x 2 + 8x + 16 = 23 - 3x
⇔ 2 x 2 + 5x - 2 = 0
Ta có: a = 2; b = 5; c = -2
Δ = b 2 - 4ac = 5 2 - 4.2.(-2) = 41 > 0
⇒ phương trình đã cho có 2 nghiệm phân biệt
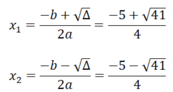
Vậy tập nghiệm của phương trình là
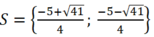

Ta có: \(\hept{\begin{cases}\left(\frac{1}{x}+y\right)+\left(\frac{1}{x}-y\right)=\frac{5}{8}\\\left(\frac{1}{x}+y\right)-\left(\frac{1}{x}-y\right)=-\frac{3}{8}\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{2}{x}=\frac{5}{8}\\2y=-\frac{3}{8}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{16}{5}\\y=-\frac{3}{16}\end{cases}}}\)

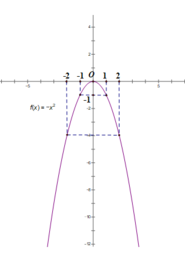
a) Lập bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y = - x 2 | -4 | -1 | 0 | -1 | -4 |
Đồ thị hàm số y = - x 2 là một đường parabol nằm phía dưới trục hoành, nhận trục Oy làm trục đối xứng, nhận gốc O (0; 0) làm đỉnh và là điểm cao nhất.
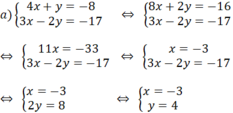
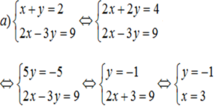
a)
Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (1; -3)