
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x^4-5x^2+4=x^4-x^2-(4x^2-4) = x^2(x^2-1)-4(x^2-1)
=(x^2-4)(x^2-1)
=(x-2)(x+2)(x-1)(x+1)
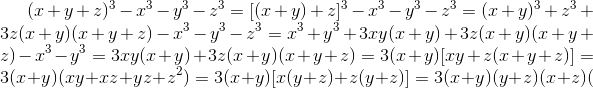

g, sửa đề
\(5x^2-5xy+7y-7x=5x\left(x-y\right)+7\left(y-x\right)=\left(5x-7\right)\left(x-y\right)\)
h, sửa đề
\(xy-xz+z-y=x\left(y-z\right)-\left(y-z\right)=\left(x-1\right)\left(y-z\right)\)
i, \(x^3+2x^2-3x-6=x^2\left(x+2\right)-3\left(x+2\right)=\left(x^2-3\right)\left(x+2\right)\)

a ) \(4x^2-y^2+4x+1\)
= \(\left(4x^2+4x+1\right)-y^2=\left(2x+1\right)^2-y^2=\left(2x+1+y\right).\left(2x+1-y\right)\)
b ) \(x^3-x+y^3-y\)
= \(\left(x^3+y^3\right)-\left(x+y\right)\)
= \(\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x+y\right)\)
= \(\left(x+y\right)\left(x^2-xy+y^2-1\right)\)
Chúc bạn học tốt !!!
\(a.\)\(4x^2-y^2+4x+1\)
\(=\left(4x^2+4x+1\right)-y^2\)
\(=\left(2x+1\right)^2-y^2\)
\(=\left(2x+1+y\right)\left(2x+1-y\right)\)

6, x mũ 4 - 4x mũ 3 - 8x mũ 2 + 8x =x (x+2) (x^2-6x+4)
8, x mũ 4 + 2x mũ 3 + x mũ 2 - y mũ 2 = -(y-x^2-x) (y+x^2+x)
10, 4x mũ 2 ( x + y ) -x - y = (2x-1) (2x+1) (y+x)

f) = x2( x - 4 ) - 9( x - 4 ) = ( x - 4 )( x - 3 )( x + 3 )
g) = 4( x - y ) + ( x - y )2 = ( x - y )( x - y + 4 )
h) = x3( x + 1 ) + ( x - 1 )( x + 1 ) = ( x + 1 )( x3 + x - 1 )
i) = ( x - y )( x + y ) - 4( x + y ) = ( x + y )( x - y - 4 )
j) = ( x - y )( x2 + xy + y2 ) - 3( x - y ) = ( x - y )( x2 + xy + y2 - 3 )
Trả lời:
f, x3 - 4x2 - 9x + 36 = ( x3 - 4x2 ) - ( 9x - 36 ) = x2 ( x - 4 ) - 9 ( x - 4 ) = ( x - 4 )( x2 - 9 ) = ( x - 4 )( x - 3 )( x + 3 )
g, 4x - 4y + x2 - 2xy + y2 = ( 4x - 4y ) + ( x2 - 2xy + y2 ) = 4 ( x - y ) + ( x - y )2 = ( x - y ) ( 4 + x - y )
h, x4 + x3 + x2 - 1 = ( x4 + x3 ) + ( x2 - 1 ) = x3 ( x + 1 ) + ( x - 1 )( x + 1 ) = ( x + 1 )( x3 + x - 1 )
i, x2 - y2 - 4x - 4y = ( x2 - y2 ) - ( 4x + 4y ) = ( x - y )( x + y ) - 4 ( x + y ) = ( x + y )( x - y - 4 )
j, x3 - y3 - 3x + 3y = ( x3 - y3 ) - ( 3x - 3y ) = ( x - y )( x2 + xy + y2 ) - 3 ( x - y ) = ( x - y )( x2 + xy + y2 - 3 )

\(a,x^2+4x-y^2+4\)
\(=\left(x^2+4x+4\right)-y^2\)
\(=\left(x+2\right)^2-y^2\)
\(=\left(x+2-y\right)\left(x+2+y\right)\)
\(b,25-4x^2-4xy-y^2\)
\(=25-\left(4x^2+4xy+y^2\right)\)
\(=5^2-\left(2x+y\right)^2\)
\(=\left(5-2x+y\right)\left(5+2x+y\right)\)
\(c,x^3-x+y^3-y\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2+1\right)\)

\(a,x^2+7x+7y-y^2\)
\(=x^2-y^2+7\left(x+y\right)\)
\(=\left(x-y\right)\left(x+y\right)+7\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+7\right)\)
\(b,x^2-2x-9y^2+6y\)
\(=x^2-\left(3y\right)^2-2\left(x-3y\right)\)
\(=\left(x-3y\right)\left(x+3y\right)-2\left(x-3y\right)\)
\(=\left(x-3y\right)\left(x+3y-2\right)\)
\(c,x^2-xy+x^3-3x^{2y}+3x^{2y}-y^3\)
\(=x\left(x-y\right)+\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=\left(x-y\right)\left(x+x^2+xy+y^2\right)\)
đầu tiên là bạn có thể ghi là ^3
mn gợi ý nhé, chứng minh (x+y+z)3 = x3 + y3 + z3 + 3(x+y)(y+z)(x+z)
[x+(y+z)]3 ik. còn đoạn 3(x+y)(y+z)(x+z) thì khi tách rút 3 r phân tích