Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Chú ý E tỉ lệ thuận với n. Chuẩn hóa R = 1. Áp dụng công thức tính ![]()

Khi ω = ω 1 mạch xảy ra cộng hưởng, chuẩn hóa R = 1 Z L = Z = 1
Khi ω = 2 ω 1 thì
P = 4 U 2 R cos 2 φ = 2 5 U 2 R ⇒ cos φ = 1 10
c o s φ = 1 10 = 1 1 + 2 X − X 2 2 ⇒ X = 2
Khi ω = 3 ω 1 thì hệ số công suất của mạch sẽ là:
c o s φ = 1 1 + 3 X − X 3 2 = 3 265
Đáp án B

Đáp án: D
Điện áp từ máy phát cấp cho mạch là: u = U 0 cos ω t (giả sử chọn điều kiện ban đầu sao cho φ = 0 ); với U 0 = E 0 = N Φ 0 ω = U 2
⇒ U = k ω ; với k = N Φ 0 2
Công suất tiêu thụ là
P = R I 2 = U 2 R R 2 + L ω 2 = k ω 2 R R 2 + L ω 2
Với ω 1 = n thì
P 1 = R k n 2 R 2 + L n 2 = 16 ⇒ 1 16 = R 2 R k n 2 + L n 2 R k n 2 ( 1 )
Với ω = 2 n thì
P 2 = R 2 k n 2 R 2 + 2 L n 2 = 20 ⇒ 1 20 = R 2 4 R k n 2 + 4 L n 2 R k n 2 ( 2 )
Với ω 3 = 3 n thì
P 3 = R 3 k n 2 R 2 + 3 L n 2 ⇒ 1 P 3 = R 2 9 R k n 2 + 9 L n 2 R k n 2 ( 3 )
Từ (1) và (2)
⇒ R 2 R k n 2 = 1 60 và
L n 2 R k n 2 = 2 , 75 60 ⇒ P 3 = 20 , 97 W.

Chọn đáp án D.
Điện áp từ máy phát cấp cho mạch là: ![]() (giả sử chọn điều kiện ban đầu sao cho
(giả sử chọn điều kiện ban đầu sao cho ![]() ) ; với
) ; với
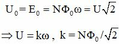
Công suất tiêu thụ là
P= 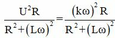
= 20,7W

Giải thích: Đáp án C
*Công suất tiêu thụ của đoạn mạch RL khi nối vào máy phát điện xoay chiều một pha.

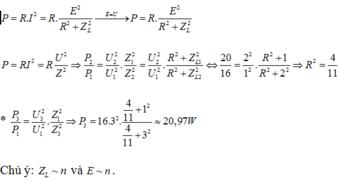

Đáp án A
Ta có: E = ωΦ = 2πfΦ = 2π.np.Φ => E tỉ lệ thuận với n.
ZL = ωL = 2πf.L = 2π.np.L => E tỉ lệ thuận với n.
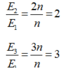
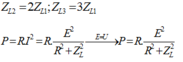
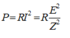
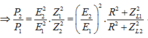
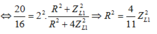
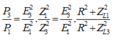
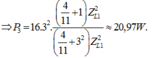

Đáp án B
+ Máy phát điện có E tỉ lệ thuận với ![]()
Có ![]()
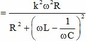
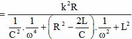
Để P max thì mẫu số phải min. Để ý thấy mẫu số là dạng tam thức bậc 2, nên mẫu số min khi và chỉ khi ![]()
Mặt khác, có 2 giá trị
ω
1
và
ω
2
làm P bằng nhau nên chúng sẽ thỏa mãn định lý Viete: 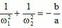
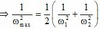
Có ![]()
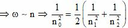
![]() (vòng/phút)
(vòng/phút)

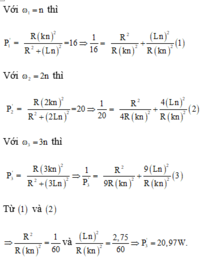

Công suất của mạch ngoài \(P = I^2 R = \frac{E^2}{R^2+(Z_L-Z_C)^2}R\)
Mà suất điện động hiệu dụng \(E = \omega\Phi \)
TH1: \(\omega = \omega_0; P_{max}\)
\(P = I^2 R = \frac{E^2}{R^2+(Z_L-Z_C)^2}R\)
\( = \frac{\omega^2 \Phi ^2}{R^2+(Z_L-Z_C)^2}R \)
\( = \frac{ \Phi ^2}{\frac{R^2}{\omega^2}+\frac{Z_L^2}{\omega^2}-2\frac{Z_LZ_C}{\omega^2}+\frac{Z_C^2}{\omega^2}}R \)
\( = \frac{ \Phi ^2}{\frac{1}{\omega^4C^2}+\frac{R^2-2L/C}{\omega^2}+L^2}R \)
\(P_{max} \Leftrightarrow A = (\frac{1}{\omega^4C^2}+\frac{R^2-2L/C}{\omega^2}+L^2)_{min}\)
đặt \(x = \frac{1}{\omega^2}\)
=> \(A_{min} \Leftrightarrow x = \frac{-b}{2a} = \frac{2L/C-R^2}{2/C^2}.\)
=> \(\frac{2}{C^2\omega_0^2} = \frac{2L}{C}-R^2\) hay \(2Z_C^2 = 2Z_LZ_C - R^2 => R^2 =2Z_LZ_C- 2Z_C^2.(1)\)
Ta có \(\frac{P_1}{P_0} = \frac{I_1^2}{I_0^2} = \frac{E_1^2Z_0^2}{E_0^2Z_1^2} = \frac{\omega_1^2Z_0^2}{\omega_0^2Z_1^2} = \frac{4\omega_0^2Z_0^2}{\omega_0^2Z_1^2} = \frac{1}{2}\)
=> \(Z_1^2 = 8Z_0^2\)
=> \(R^2 +(2Z_L - \frac{Z_C}{2})^2 = 8 (R^2 + (Z_L-Z_C)^2) (2)\)
Thay (1) vào (2) ta được \(4Z_L^2 -\frac{7Z_C^2}{4} = 8(Z_L^2 - Z_C^2)\)
=> \(\frac{25}{4}Z_C^2 = 4Z_L^2\) hay \(Z_L = \frac{5}{4}Z_C .(3)\)
Tiếp theo ta xét tỷ số \(\frac{P_2}{P_0} = \frac{\omega_2^2 Z_0^2}{\omega_0^2Z_2^2} = \frac{9.(R^2+(Z_L-Z_C)^2)}{R^2+(3Z_L-Z_C/3)^2}=\frac{9(Z_L^2 - Z_C^2)}{9Z_L^2 - 17/9Z_C^2} = \frac{9(25/4-1)}{9.25/4 - 17/9} = \frac{81/16}{1753/144} = \frac{729}{1753}.\)
=> \(P_2 = \frac{729}{1753}P_0\)
Đáp án thu được như của bạn rồi nhé.
Mình gõ nhầm đoạn tính ở dòng cuối nhé.
\(\frac{P_2}{P_0} = \frac{9.(25/16 - 1)}{9.25/16 - 17/9} = \frac{729}{1753}.\)
Bạn xem lại kết quả nhé. Mình cũng bầm lại rồi nhưng không thu được kết quả của bạn.:)))))