
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,\Leftrightarrow\left\{{}\begin{matrix}m+2=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\\ c,\text{PT giao Ox: }y=0\Leftrightarrow\left(m+2\right)x-m=0\\ \text{Thay }x=2\Leftrightarrow2m+4-m=0\\ \Leftrightarrow m=-4\\ d,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{m}{m+2}\Leftrightarrow A\left(\dfrac{m}{m+2};0\right)\Leftrightarrow OA=\left|\dfrac{m}{m+2}\right|\\ x=0\Leftrightarrow y=-m\Leftrightarrow B\left(0;-m\right)\Leftrightarrow OB=\left|m\right|\\ \Delta OAB\text{ cân }\Leftrightarrow OA=OB\Leftrightarrow\left|\dfrac{m}{m+2}\right|=\left|m\right|\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{m}{m+2}=m\\\dfrac{m}{m+2}=-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\left(m+1\right)=0\\m\left(m+3\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\\m=-3\end{matrix}\right.\)

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp

Bài 2:
a: Thay x=-2 và y=-1 vào (d), ta được:
-2(m+1)+m+2=-1
=>-2m-2+m+2=-1
=>-m=-1
=>m=1
b: (d): y=2x+3
Tọa độ A là:
y=0 và 2x+3=0
=>x=-3/2 và y=0
=>OA=1,5
Tọa độ B là:
x=0 và y=2*0+3=3
=>OB=3
\(AB=\sqrt{1.5^2+3^2}=1.5\sqrt{5}\)
=>\(C=1.5+3+1.5\sqrt{5}=1.5\sqrt{5}+4.5\)
\(S=\dfrac{1}{2}\cdot OA\cdot OB=2.25\)

\(\dfrac{x-2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

4:
a: góc CEH+góc CDH=180 độ
=>CDHE nội tiếp
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
góc EHA=góc DHB
=>ΔHEA đồng dạng với ΔHDB
=>HE/HD=HA/HB
=>HE*HB=HD*HA

\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)

a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14

\(P=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : x > 0
\(=\left(\frac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{1}{\sqrt{x}+1}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{x-1}=\frac{x-2\sqrt{x}+1}{x-1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)



 mọi người giải hộ em với ạ,em cảm ơn
mọi người giải hộ em với ạ,em cảm ơn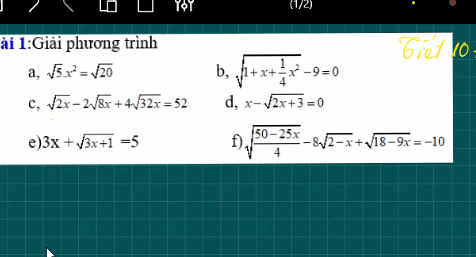


Theo Dirichlet, trong 3 số a;b;c luôn có 2 số cùng phía so với 1, giả sử đó là a và b
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\Leftrightarrow ab+1\ge a+b\)
\(\Rightarrow2ab+2\ge ab+a+b+1=\left(a+1\right)\left(b+1\right)\)
\(\Rightarrow2\left(ab+1\right)\left(c+1\right)\ge\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
\(\Rightarrow\frac{2}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge\frac{1}{\left(ab+1\right)\left(c+1\right)}=\frac{1}{\left(\frac{1}{c}+1\right)\left(c+1\right)}=\frac{c}{\left(c+1\right)^2}\)
Mặt khác ta lại có:
\(\left(a+1\right)^2=\left(\sqrt{ab}.\sqrt{\frac{a}{b}}+1.1\right)^2\le\left(ab+1\right)\left(\frac{a}{b}+1\right)=\frac{\left(ab+1\right)\left(a+b\right)}{b}\)
\(\Rightarrow\frac{1}{\left(a+1\right)^2}\ge\frac{b}{\left(ab+1\right)\left(a+b\right)}\)
Tương tự: \(\frac{1}{\left(b+1\right)^2}\ge\frac{a}{\left(ab+1\right)\left(a+b\right)}\Rightarrow\frac{1}{\left(a+1\right)^2}+\frac{1}{\left(b+1\right)^2}\ge\frac{1}{ab+1}=\frac{1}{\frac{1}{c}+1}=\frac{c}{c+1}\)
Do đó:
\(VT=\frac{1}{\left(a+1\right)^2}+\frac{1}{\left(b+1\right)^2}+\frac{1}{\left(c+1\right)^2}+\frac{2}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\)
\(VT\ge\frac{c}{c+1}+\frac{1}{\left(c+1\right)^2}+\frac{c}{\left(c+1\right)^2}=\frac{c\left(c+1\right)+1+c}{\left(c+1\right)^2}=\frac{\left(c+1\right)^2}{\left(c+1\right)^2}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)