Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Không gian mẫu là “Chọn ngẫu nhiên 2 người từ 10 học sinh trong tổ đó”. Suy ra số phần tử trong không gian mẫu là n ( Ω ) = C 10 2
Gọi A là biến cố “2 người được chọn là nữ” thì kết quả thuận lợi cho biến cố A là n ( A ) = C 3 2
Vậy xác suất cần tính là P ( A ) = n ( A ) n ( Ω ) = C 3 2 C 10 2 = 1 15 .

a) chia 12 ghế thành 2 ô, nam ở một ô, nữ ở 1 ô. do vậy có 2 cách sắp xếp cho nam và nữ
sắp xếp các bạn nam ngồi vào ghế có chỉnh hợp chập 6 của 6 cách
tương tự, các bạn nữ cũng có chỉnh hợp chập 6 của 6 cách
như vậy có 2 nhân chỉnh hợp chập 6 của 6 nhân chỉnh hợp chập 6 của 6 bằng 1036800
chắc vậy. Bạn hỏi bọn 11 sẽ ổn hơn

Vì trong hộp có tổng cộng 40 que, trong đó có 1 que màu đỏ và 39 que màu trắng, nên xác suất để rút được que màu đỏ trong lần rút đầu tiên là 1/40.
Sau khi rút được que màu đỏ, số que trong hộp giảm còn 39, trong đó có 1 que màu đỏ và 38 que màu trắng. Xác suất để rút được que màu đỏ trong lần rút thứ hai là 1/39.
Tương tự, xác suất để rút được que màu đỏ trong lần rút thứ ba là 1/38, và tiếp tục như vậy.
Vậy, xác suất để rút được que màu đỏ trong lần rút thứ k là 1/(40-k+1).
Để tìm số thứ tự có khả năng trúng thưởng cao nhất, ta cần tìm giá trị k sao cho xác suất 1/(40-k+1) là lớn nhất.
Để tìm giá trị k, ta có thể tìm giá trị lớn nhất của 40-k+1, tức là giá trị nhỏ nhất của k.
Vì 40-k+1 là giá trị lớn nhất, nên ta có:
40-k+1 ≥ 40
-k+1 ≥ 0
k ≤ 1
Vậy, giá trị nhỏ nhất của k là 1.
Vậy, số thứ tự có khả năng trúng thưởng cao nhất là 1.

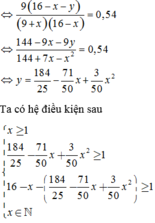
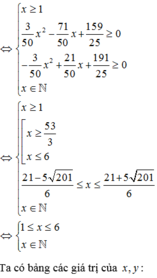





minh châu nói cx đúng
giải giùm em đi m.n ơi