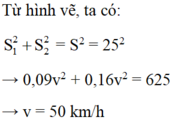Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đinh lý Pytago: \(\left(30\sqrt{2}\cdot cos45^o\right)-20=10m\)
Về phía Nam.
Chọn C.

1.
Quãng đường đi được của ô tô là: 6 + 4 + 3 = 13 (km)
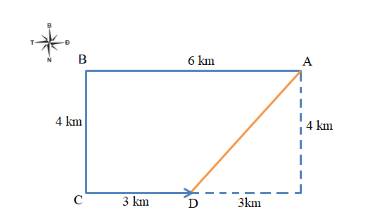
Độ dịch chuyển: AD
Ta có: BH = CD = 3 km; HD = BC = 4 km; AH = AB - BH = 6 - 3 = 3 km
=> \(AD = \sqrt {A{H^2} + H{D^2}} = \sqrt {{3^2} + {4^2}} = 5(km)\) (theo hướng Tây - Nam)
2.
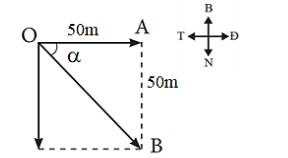
Người bơi ngang từ bờ bên này sang bên kia theo dự định là OA = 50 m.
Thực tế, do nước sông chảy mạnh nên vị trí của người đó ở vị trí B, ta có AB = 50 m
=> Độ dịch chuyển: \(OB = \sqrt {O{A^2} + A{B^2}} = \sqrt {{50^2} + {50^2}} = 70,7(m)\).
(450 Đông – Nam)

Bài này không khó đâu, cứ theo từng giai đoạn mà vẽ nhé.
a) Đồ thị biểu diễn quỹ đạo của tàu.
x(km) y(km) O 8 M 14,1 5 P N
b) Tàu dừng lại tại vị trí P
Toạ độ của N là: \(x_N=14,1.\cos 45^0=10\) ; \(y_N=8+14,1.\cos45^0=18\),
Toạ độ của P là: \(x_P=x_N+5=15\) ; \(y_P=y_N=18\)
Vậy khoảng cách từ O đến nơi tàu dừng lại là: \(d=\sqrt{x_P^2+y_P^2}=\sqrt{15^2+18^2}\approx 23,43(km)\)
c) Theo câu B ta có toạ độ vị trí tàu dừng là \((15;18)\)

Chọn A.
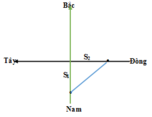
Gọi vận tốc của ca nô là v km/h.
Đổi 18 phút = 0,3 giờ, 24 phút = 0,4 giờ
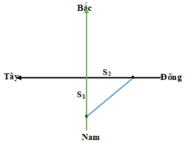
Quãng đường mà ca nô đi được theo hướng Nam - Bắc là: S1 = 0,3.v
Quãng đường mà ca nô đi được theo hướng Đông - Tây là: S2 = 0,4.v
Từ hình vẽ, ta có: = S2 = 252
→ 0,09v2 + 0,16v2 = 625 → v = 50 km/h

Chọn A.
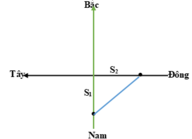
Gọi vận tốc của ca nô là v km/h.
Đổi 18 phút = 0,3 giờ, 24 phút = 0,4 giờ
Quãng đường mà ca nô đi được theo hướng Nam - Bắc là: S 1 = 0,3.v
Quãng đường mà ca nô đi được theo hướng Đông - Tây là: S 2 = 0,4.v
Từ hình vẽ, ta có: S 1 2 + S 2 2 = S 2 = 25 2
→ 0,09 v 2 + 0,16 v 2 = 625
→ v = 50 km/h