Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(\overrightarrow{v};\overrightarrow{v_1};\overrightarrow{v_2}\) lần lượt là vận tốc của viên đạn ban đầu, của mảnh đạn 1kg và mảnh đạn 2kg sau khi bắn
Động lượng ban đầu của viên đạn là
\(\overrightarrow{p_0}=3\overrightarrow{v}\)
Động lượng sau của hệ là
\(\overrightarrow{p_s}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
Do động lượng được bảo toàn nên
\(\overrightarrow{p_0}=\overrightarrow{p_s}\) ⇒ \(3\overrightarrow{v}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
⇒ \(\overrightarrow{v_1}=3\overrightarrow{v}-2\overrightarrow{v_2}\)
⇒ v12 = 9.v2 + 4v22 - 12 . v . v2 . cos (45)
⇒ v12 = 9 . 472 + 4.502 - 12 . 47 . 50 . \(\dfrac{\sqrt{2}}{2}\)
⇒ v1 = 99,7 (m/s)
\(3\overrightarrow{v}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
⇒ \(2\overrightarrow{v_2}=3\overrightarrow{v}-\overrightarrow{v_1}\)
⇒ cos \(\left(\overrightarrow{v};\overrightarrow{v_1}\right)\) = 0.789
⇒ \(\left(\overrightarrow{v};\overrightarrow{v_1}\right)\) = 37054'
Vậy mảnh đạn 1 bay theo chiều dương và hợp với phương thẳng đứng 1 góc 37054' có độ lớn là 99,7 m/s

sao m=m1=3kg thế kia khác gì nó không nổ không??? :D xem lại đề bài rồi dựa vào cách làm mình nhá
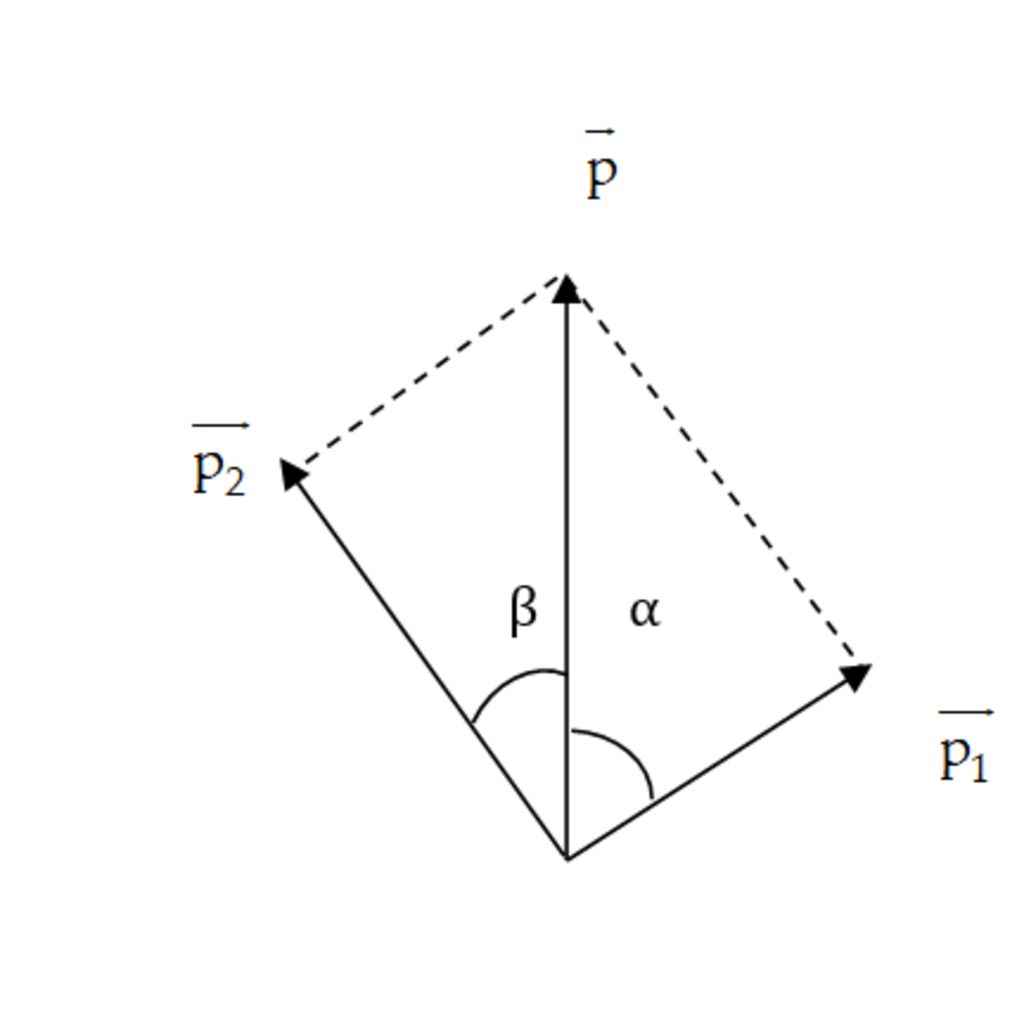
Áp dụng định lý hàm cos trong tam giác ta có:
\(p_2^2=p^2+p_1^2-2p.p_1.\cos\left(45^0\right)\)
\(\Leftrightarrow p_2=\sqrt{p^2+p_1^2-2p.p_1\cos\left(45^0\right)}=\sqrt{\left(m.v\right)^2+\left(m_1.v1\right)^2-2mv\left(m_1v_1\right)\dfrac{\sqrt{2}}{2}}=......\) từ đó suy ra được \(v_2=\dfrac{p_2}{m_2}=.......\left(m/s\right)\)
Áp dụng hệ quả định lý hàm cos: gọi \(\beta\) là góc hợp bởi mảnh thứ 2 với phương thẳng đứng.
\(\cos\beta=\dfrac{p_2^2+p^2-p_1^2}{2p_2p}=......\)

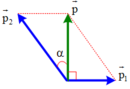
Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
+ Với p = m v = 2.250 = 500 k g . m / s p 1 = m 1 v 1 = 1.500 = 500 k g . m / s p 2 = m 2 v 2 = v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 k g m / s
+ Mà sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 45 ° với vận tốc 500 2 m / s (m/s)
Chọn đáp án A

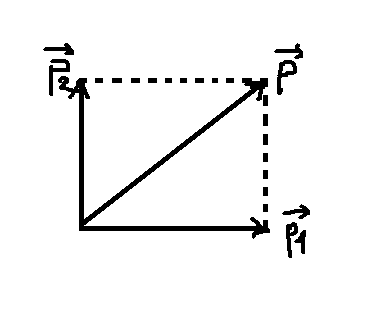
a)Vận tốc viên đạn trước khi nổ:
\(tan45^o=\dfrac{p}{p_1}=\dfrac{m\cdot v}{m_1\cdot v_1}=\dfrac{2\cdot v}{0,5\cdot400}\)
\(\Rightarrow v=100\)m/s
Vận tốc mảnh đạn lớn:
\(sin45^o=\dfrac{p_1}{p_2}=\dfrac{m_1\cdot v_1}{m_2\cdot v_2}=\dfrac{0,5\cdot400}{\left(2-0,5\right)\cdot v_2}\)
\(\Rightarrow v_2=188,56\)m/s

Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(p_1=m_1v_1=1\cdot100=100kg.m\)/s
\(p=\left(m_1+m_2\right)\cdot V=\left(1+3\right)\cdot200=800kg.m\)/s
Động lượng mảnh thứ hai:
\(p_2=p-p_1=800-100=700kg.m\)/s
Vận tốc mảnh nhỏ:
\(v_2=\dfrac{p_2}{m_2}=\dfrac{700}{3}=233,33\)m/s

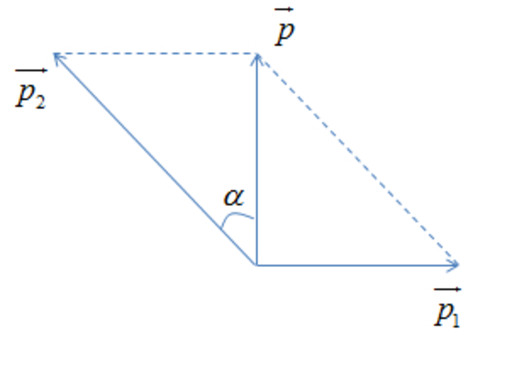
Bảo toàn động lượng ta có:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p^2=p_1^2+p_2^2+2\cdot p_1\cdot p_2\cdot cos\left(\overrightarrow{p_1;}\overrightarrow{p_2}\right)\) (1)
Có \(p=m\cdot v=2\cdot250=500\)kg.m/s
\(p_1=m_1\cdot v_1=1\cdot250=250kg.\)m/s
\(\left(1\right)\Rightarrow500^2=250^2+p_2^2+2\cdot250\cdot p_2\cdot cos60^o\)
\(\Rightarrow187500=p_2^2+250p_2\)
\(\Rightarrow\left[{}\begin{matrix}p_2\approx325,7\\p_2\approx-575,7\left(loại\right)\end{matrix}\right.\)
Theo hình ta có:
\(p_1\cdot cos\alpha=p_2\cdot sin\beta\)
\(\Rightarrow sin\beta=\dfrac{p_1\cdot cos\alpha}{p_2}=\dfrac{250\cdot cos\left(90-30\right)}{325,7}=0,38\)
\(\Rightarrow\beta\approx22,57^o\)
Mảnh thứ hai bay theo góc \(22,57^o\)

Refer:
\(m=2kg,v=250m/s,v_1=250m/s,α=60^o \)
Động lượng của viên đạn ban đầu:
\(p=m.v=2.250=500kg.m/s\)Động lượng của các mảnh :\(p_1=m_1.v_1=\dfrac{2}{2}.250=250(kg.m/s)\)
\(p_2=m_2.v_2=\dfrac{2}{2}.v_2=v_2(kg.m/s)\)
theo quy tắc hình bình hành ta có:
\(p_2=\sqrt{p_2+p^2_1+2.p.p_1.cosα}\)
\(=\sqrt{500^2+250^2+2.500.250.cos60}\)
\(=661,4(kg.m/s)\)
Vận tốc của mảnh 2:
\(p_2=v_2\Rightarrow v_2=661,4m/s\)Bay theo phương hợp với phương thẳng đứng:\(\dfrac{P}{sin α}=\dfrac{P_1}{sin β} \)
\(\Rightarrow sinβ=\dfrac{sin60.250}{500}=\dfrac{\sqrt{3}}{4} \)
\(\Rightarrow β=25^o39' \)
dạng này mình mới làm xong một bài nhé, bạn có thể lướt xuống tham khảo rồi áp dụng, không nên đăng cùng một loại câu hỏi nhiều lần
bài này đã cho bạn cái sườn hồi tối rồi :D xin phép giải vắn tắt nhất
\(p_2=\sqrt{p^2+p_1^2-2.p.p_1.\cos\left(45^0\right)}\) \(=\sqrt{\left(mv\right)^2+\left(m1v1\right)^2-2mv\left(m1v1\right)\dfrac{\sqrt{2}}{2}}\)
\(\Rightarrow p_2=m_2v_2\simeq999,14\left(kg.m/s\right)\)\(\Rightarrow v_2=\dfrac{p_2}{m_2}\simeq999,14\left(m/s\right)\) :D
\(\cos\beta=\dfrac{p_2^2+p^2-p_1^2}{2p_2p}\) thay số nốt :D
mọi thắc mắc truy cập:
https://hoc24.vn/cau-hoi/mot-vien-dan-co-khoi-luong-3kg-bay-len-theo-phuong-thang-dung-voi-v-471ms-thino-thanh-2-manh-manh-1-co-khoi-luong-3kg-van-toc-overrightarrowv-1-chech-theo-phuong-thang-dung-1-goc-450-voi-d.334563063787