Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Áp dụng định luật II Niuton ta có: mgsina - mmgcosa = ma
=> gsin300 - 0,1x.cos300 = a => 5 - 3 2 x = a = x ' '
+ Đặt:
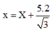
Ta có:
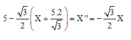
+ Phương trình trên có nghiệm là X = A cos ( 3 2 t + φ ) => v = - A 3 2 sin ( 3 2 t + φ )
+ Khi t = 0 thì v = 0 => j = 0 => v = - A 3 2 sin ( 3 2 t )
+ Khi dừng lại thì v = 0 => sin 3 2 t = 0 → t = 2 k π 3
+ Cho các giá trị của k và so đáp án ta được đáp án

Đáp án B
+ Áp dụng định luật II Niuton ta có: mgsina - mmgcosa = ma
=> gsin300 - 0,1x.cos300 = a => 5 - 3 2 x = a = x ' '
Đặt:

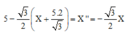
+ Phương trình trên có nghiệm là X = A cos ( 3 2 t + φ ) => v = - A 3 2 sin ( 3 2 t + φ )
+ Khi t = 0 thì v = 0 => j = 0 => v = - A 3 2 sin ( 3 2 t )
+ Khi dừng lại thì v = 0 => sin 3 2 t = 0 → t = 2 k π 3
+ Cho các giá trị của k và so đáp án ta được đáp án

Chọn đáp án B
+ Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
+ Độ giảm biên độ của vật sau một lần qua VTCB:
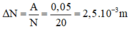
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB:
![]()

Theo định luật ll Niu tơn:
\(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Gia tốc vật:
\(a=-g\left(sin\alpha+k\cdot cos\alpha\right)\)
Quãng đường vật đi được:
\(S=\dfrac{-v_0^2}{2a}=\dfrac{-v_0^2}{2g\left(sin\alpha+k\cdot cos\alpha\right)}\)

60 P N
Trong trường hợp này chỉ có duy nhất một sự khác biệt: Ở vị trí cân bằng mới, vật cách VTCB cũ là x0 thì:
\(kx_0=\mu N=\mu mg\cos60^0\Leftrightarrow x_0=\frac{\mu mg\cos60^0}{k}\)
Độ giảm biên độ sau mỗi chu kì là: \(4x_0=\frac{4\mu mg\cos60^0}{k}\)
Bài này không có m và k nên theo gợi ý này bạn làm tiếp nhé.
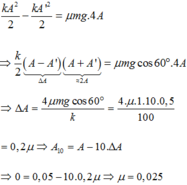
NPFms0yx
Áp dụng định luật II Niuton ta có: \(\overrightarrow{P}+ \overrightarrow{F_{ms}} + \overrightarrow{N} = m\overrightarrow{a}\)
chiếu lên Ox: \(P \sin \alpha - F_{ms} = ma.(1)\)
chiếu lên Oy: \(-P \cos \alpha + N = 0\) => \(N = P\cos \alpha.\) Thay vào phương trình (1) ta được
=> \(g \sin \alpha - 0,1.x.\cos \alpha = a\) (do \(F_{ms} = \mu N = 0,1.x.P\sin \alpha.\))
=> \(x'' + g\cos \alpha .0,1x - g\sin \alpha = 0.\)(do \(a = x'')\)
=> \(x'' + g\cos \alpha .0,1(x - 10\tan \alpha) = 0.\)
Đặt \(X = x- 10 \tan \alpha\) => \(X''(t) = x''(t)\)
=> \(X(t)'' + g\cos \alpha .0,1.X(t) = 0.\)
Phương trình có nghiệm là: \(X(t) = A\cos (\omega t+ \varphi)\); \(\omega = \sqrt{0,1.g.\cos \alpha} = \sqrt{\frac{\sqrt{3}}{2}} \approx 0,93 rad/s.\)
0VoMN
Ban đầu vật ở đỉnh dốc có vận tốc bằng 0. Thời gian đến điểm có vận tốc bằng 0 tiếp theo là
\(t = \frac{\varphi}{\omega} = \frac{\pi}{0,93} \approx 3,375 s.\)
Chọn đáp án B.3,375s.