Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{12}=\dfrac{1}{8}+\dfrac{1}{d'}\)
\(\Leftrightarrow d'=-24\left(cm\right)\)
Chiều cao của ảnh:
\(\dfrac{d}{d'}=\dfrac{h}{h'}\Leftrightarrow h'=\dfrac{d'.h}{d}=\dfrac{-24.1}{8}=-3\left(cm\right)\)
a) Xem hình vẽ dưới đây
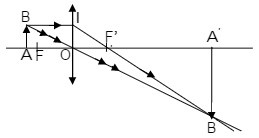
b) Theo hình trên ta đo được chiều cao của vật AB = 7 mm, chiều cao của ảnh A'B' = 21 mm = 3AB.
Hai tam giác OAB và OA'B' đồng dạng với nhau nên
= 
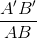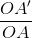(1)
Hai tam giác F'OI và F'A'B' đồng dạng với nhau nên
= = 
= 
= 
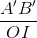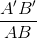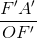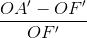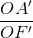- 1. (2)
Từ (1) và (2) ta có:
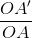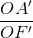= - 1
Thay các giá trị số đã cho: OA = 16 cm, OF' = 12 cm thì ta tính được OA' = 48 cm hay OA' = 3OA, từ đó tính được A'B' = 3AB, ảnh cao gấp 3 lần vật.
Hướng dẫn học sinh chọn một tỉ lệ xích thích hợp, chẳng hạn lấy tiêu cự 3 cm thì vật AB cách thấu kính 4 cm, còn chiều cao của AB là một số nguyên lần milimet, ở đây ta lấy AB là 7 cm.
a) Xem hình vẽ dưới đây
b) Theo hình trên ta đo được chiều cao của vật AB = 7 mm, chiều cao của ảnh A'B' = 21 mm = 3AB.
- Nhìn vào hình để tính xem chiều cao của vật gấp mấy lần chiều cao của ảnh.
Hai tam giác OAB và OA'B' đồng dạng với nhau nên
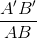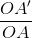= (1)
Hai tam giác F'OI và F'A'B' đồng dạng với nhau nên
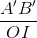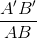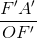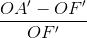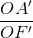= = = = - 1. (2)
Từ (1) và (2) ta có:
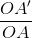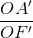= - 1
Thay các giá trị số đã cho: OA = 16 cm, OF' = 12 cm thì ta tính được OA' = 48 cm hay OA' = 3OA, từ đó tính được A'B' = 3AB, ảnh cao gấp 3 lần vật.
\(\left(1\right)\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{OI}{A'B'}\) ( do \(OI=AB\) )
mik nhầm á bạn
a. Bạn tự vẽ ( ảnh ảo )
b. Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{OI}{OA'}\) ( do OI = OA ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'+OF'}\)
\(\Leftrightarrow\dfrac{5}{OA'}=\dfrac{8}{OA'+8}\)
\(\Leftrightarrow OA'=\dfrac{40}{3}\left(cm\right)\)
Thế \(OA'=\dfrac{40}{3}\) vào \(\left(1\right)\Leftrightarrow\dfrac{2}{A'B'}=5:\dfrac{40}{3}\)
\(\Leftrightarrow A'B'=\dfrac{16}{3}\left(cm\right)\)
a) Vẽ ảnh theo đúng tỷ lệ
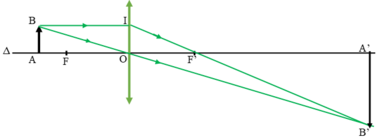
b) Trên hình vẽ, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được:
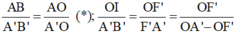
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
↔ dd' – df = d'f (1)
Chia cả hai vế của (1) cho tích d.d’.f ta được:
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 16cm, f = 12cm ta tính được: OA’ = d’ = 48cm
Thay vào (*) ta được:
Ảnh cao gấp 3 lần vật.
b) Ảnh A'B' là ảnh ảo, cùng chiều và nhỏ hơn vật AB.
c) \(\Delta OAB~\Delta OA'B'\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Rightarrow\dfrac{30}{OA'}=\dfrac{5}{A'B'}\Rightarrow\dfrac{6}{OA'}=\dfrac{1}{A'B'}\) (1)
\(\Delta FOI~\Delta FA'B'\Rightarrow\dfrac{OF}{FA'}=\dfrac{OI}{A'B'}\Rightarrow\dfrac{15}{OF-OA'}=\dfrac{AB}{A'B'}\)\(\Rightarrow\dfrac{15}{15-OA'}=\dfrac{5}{A'B'}\Rightarrow\dfrac{3}{15-OA'}=\dfrac{1}{A'B'}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{6}{OA'}=\dfrac{3}{15-OA'}\Rightarrow\dfrac{2}{OA'}=\dfrac{1}{15-OA'}\Rightarrow30-2OA'=OA'\)\(\Rightarrow3OA'=30\Rightarrow OA'=10\left(cm\right)\)
\(\Rightarrow\dfrac{6}{10}=\dfrac{1}{A'B'}\Rightarrow A'B'=\dfrac{10}{6}\approx1,667\left(cm\right)\)
Vậy khoảng cách từ ảnh tới thấu kính là 10cm, chiều cao của ảnh là khoảng 1,667cm.