Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do thời gian biến thiên vận tốc là T/4, nếu biểu diễn vận tốc bằng véc tơ quay thì góc quay là 900 nên ta có:
\((\dfrac{-20\pi\sqrt 3}{v_0})^2+(\dfrac{-20\pi}{v_0})^2=1\)
\(\Rightarrow v_0=40\pi(cm/s)\)
\(\Rightarrow \omega = \dfrac{40\pi}{10}=4\pi(rad/s)\)
\(\Rightarrow f = 2Hz\)
Chọn B.

\(F_{đh}=-k.x\Rightarrow x=\dfrac{F}{k}\)
Bảo toàn cơ năng ta có:
\(\dfrac{1}{2}mv_1^2+\dfrac{1}{2}k.x_1^2=\dfrac{1}{2}mv_2^2\) (lúc sau, lực đàn hồi = 0 thì x = 0 -> thế năng bằng 0)
\(\Rightarrow mv_1^2+k.(\dfrac{F_1}{k})^2=mv_2^2\)
Chọn C nhé bạn ![]()
\(\Rightarrow v_2^2 = v_1^2+\dfrac{F_1^2}{k.m}\)

Phương pháp: Áp dụng định luật bảo toàn động lượng
Cách giải:
Gọi vận tốc của hệ ngay sau khi va chạm là v. Áp dụng định luật bảo toàn động lượng ta có:

Đáp án A

BTNL Gọi Wt là thế năng tại vị trí S
Wt+1,8=4Wt+1,5\(\Rightarrow\) Wt = 0,1
W=1,9 Nên Wđ=1,9−9Wt=1(J). Chọn B.

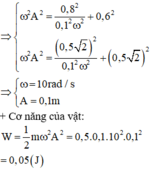

\(A^2=x^2+\frac{v^2}{\omega^2}\)
\(\frac{v^2_{max}}{\omega^2}=0.03^2+\frac{0.4^2}{\omega^2}\)
Vận tốc ở vị trí cân bằng tức là \(v_{max}=A\omega=0,5\)(m/s).
=>\(\frac{0.5^2}{\omega^2}=0.03^2+\frac{0.4^2}{\omega^2}\)
=> \(\omega=10\)(rad/s).
Hoàng Đinh để hình này luôn