Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1.
a)Tốc độ góc: \(\omega=2\pi f=2\pi\)
Ta có: \(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,05^2+\dfrac{\left(0,10\pi\right)^2}{\left(2\pi\right)^2}}=\dfrac{\sqrt{2}}{20}m\)
b)Phương trình vận tốc:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-2\pi\cdot\dfrac{\sqrt{2}}{20}sin\left(2\pi t\right)\)
Câu 2.
a)Chu kỳ: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
b)Li độ tại thời điểm \(t=2s:\)
\(x=2cos\left(5\pi t+\dfrac{\pi}{3}\right)=2cos\left(5\pi\cdot2+\dfrac{\pi}{3}\right)=1\)

Giả sử pt dao động của vật có dạng:
\(x=Acos\left(5t+\varphi\right)\left(cm\right)\)
\(\Rightarrow v=-5Asin\left(5t+\varphi\right)=5Acos\left(\dfrac{\pi}{2}+5t+\varphi\right)\left(\text{cm/s}\right)\)
Tại \(t=0:\)\(\left\{{}\begin{matrix}x=-2\left(cm\right)\\v=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=Acos\varphi=-2\left(cm\right)\\v_0=5Acos\left(\dfrac{\pi}{2}+\varphi\right)=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=-\dfrac{2}{A}\left(1\right)\\5A\left(cos\dfrac{\pi}{2}.cos\varphi-sin\dfrac{\pi}{2}.sin\varphi\right)=10\end{matrix}\right.\)
\(\Rightarrow5A.\left(-sin\varphi\right)=10\Leftrightarrow sin\varphi=\dfrac{-2}{A}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\varphi=\dfrac{-3\pi}{4}\left(rad\right);A=2\sqrt{2}\left(cm\right)\)
Vậy ta có ptdđ của vật: \(x=2\sqrt{2}cos\left(5t-\dfrac{3\pi}{4}\right)\left(cm\right)\)
b)\(v_{max}=\omega A=5A=10\sqrt{2}\left(\text{cm/s}\right)\)
\(a_{max}=\omega^2A=50\sqrt{2}\left(\text{cm/s}^2\right)\)
c) \(\alpha=\Delta t.\omega=1,4\pi.5=7\pi\left(rad\right)=6\pi+\pi\left(rad\right)\)
\(\Rightarrow S=3.4A+2\sqrt{2}-2+2\sqrt{2}+2=12A+4\sqrt{2}=28\sqrt{2}\left(cm\right)\)

Có: \(f=\dfrac{w}{2\pi}=10\Rightarrow w=20\pi\)
Phương trình dao động của vật là:
\(x=4cos\left(20\pi t-\dfrac{\pi}{2}\right)\)

Chọn đáp án C
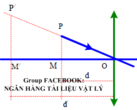
+Khi p dao động vuông góc vói trục chính, ảnh của p (và M) qua thấu kính là ảnh ảo, số phóng đại dưomg k = 2.
k = f f − d ⇒ d = 1 − 1 k f = f 2 = 7 , 5 c m
+ Vậy M cách thấu kính 7,5cm
+ Khi P dao động dọc theo trục chính với biên độ 2,5cm
+ P ở biên phải M thì d 1 = 5 c m
d 1 / = d 1 f d 1 − f = 5.15 5 − 15 = − 7 , 5 c m
+ P ở biên trái M thì d 2 = 10 c m d 1 / = d 1 f d 1 − f = 10.15 10 − 15 = − 30 c m
+ Độ dài quỹ đạo của ảnh P’ là L = 2A = 30 - 7,5 = 22,5 (cm).
+ Tần số dao động là 5 Hz, chu kì dao động là T = 0,2 s.
+ Tốc độ trung bình của ảnh P’ trong khoảng thời gian 0,2 s là
v t b = 4 A T = 2.22 , 5 0 , 2 = 225 c m / s = 2 , 25 m / s

Thời gian ngắn nhất để vật đi từ VTCB đến li độ \(x=-\dfrac{A}{2}\) là \(\dfrac{T}{12}\)
\(\Rightarrow\dfrac{T}{12}=0,1\Rightarrow T=1,2\left(s\right)\)

\(f=5Hz=>\omega=\dfrac{2\pi}{f}=\dfrac{2\pi}{5}
\\
A^2=x^2+\dfrac{v^2}{\omega^2}\\
< =>v^2=\omega^2\left(A^2-x^2\right)\\
< =>v^2=\dfrac{2\pi}{5}\left(4^2-2^2\right)\\
< =>v^2=\dfrac{24\pi}{5}\\
< =>v=\dfrac{2\sqrt{6}\pi}{5}\)
\(a=A\omega^2\\
< =>a=4.\left(\dfrac{2\pi}{5}\right)^2\\
< =>a=\dfrac{16\pi}{25}\)
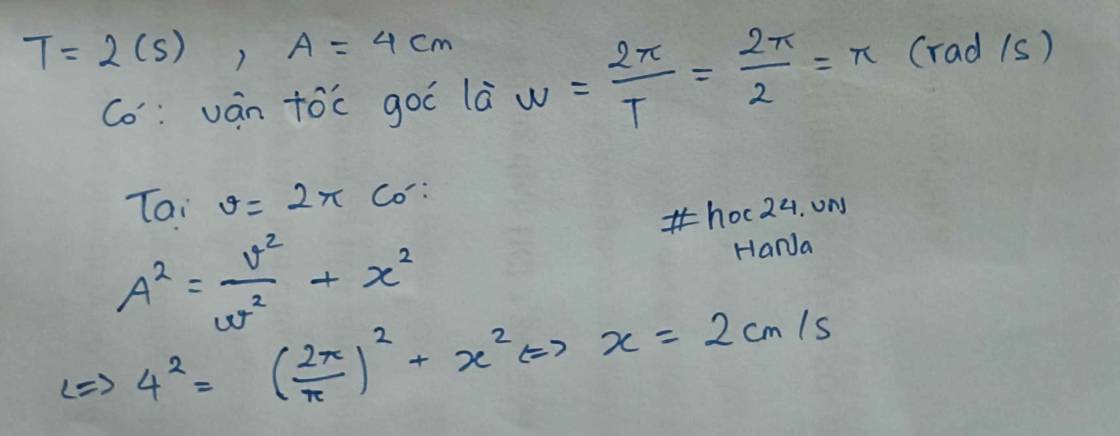
Ta có: \(x^2+\dfrac{v^2}{w^2}=A^2\)
\(\Rightarrow A^2=0,24^2+\dfrac{2,8^2}{40^2}=\dfrac{1}{16}\\ \Rightarrow A=0,25\left(m\right)=25cm\)