Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Chu kì: \(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,2}{200}}=0,2s\Rightarrow\omega=\dfrac{2\pi}{T}=10\pi\)
Vật qua vị trí \(x=1,5=\dfrac{A}{2}\) theo chiều dương nên \(\varphi=-\dfrac{\pi}{3}\).
PT dao động của vật: \(x=Acos\left(\omega t+\varphi\right)=3cos\left(10\pi-\dfrac{\pi}{3}\right)\left(cm\right)\)
b)Tại \(t=1s\) thì:
Vận tốc vật:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi\cdot3\cdot sin\left(10\pi t-\dfrac{\pi}{3}\right)=-30\pi sin\left(10\pi t-\dfrac{\pi}{3}\right)\)
\(\Rightarrow v=-30\pi sin\left(10\pi\cdot1-\dfrac{\pi}{3}\right)\approx81,62cm/s\)
Gia tốc vật:
\(a=-\omega^2Acos\left(\omega t+\varphi\right)=-3000cos\left(10\pi t-\dfrac{\pi}{3}\right)\left(cm/s^2\right)\)
\(\Rightarrow a=-3000cos\left(10\pi\cdot1-\dfrac{\pi}{3}\right)=-1500\left(cm/s^2\right)\)

Có: \(f=\dfrac{w}{2\pi}=10\Rightarrow w=20\pi\)
Phương trình dao động của vật là:
\(x=4cos\left(20\pi t-\dfrac{\pi}{2}\right)\)

Câu 1.
a)Tốc độ góc: \(\omega=2\pi f=2\pi\)
Ta có: \(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,05^2+\dfrac{\left(0,10\pi\right)^2}{\left(2\pi\right)^2}}=\dfrac{\sqrt{2}}{20}m\)
b)Phương trình vận tốc:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-2\pi\cdot\dfrac{\sqrt{2}}{20}sin\left(2\pi t\right)\)
Câu 2.
a)Chu kỳ: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
b)Li độ tại thời điểm \(t=2s:\)
\(x=2cos\left(5\pi t+\dfrac{\pi}{3}\right)=2cos\left(5\pi\cdot2+\dfrac{\pi}{3}\right)=1\)

Phương trình dao động của vật là: \(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
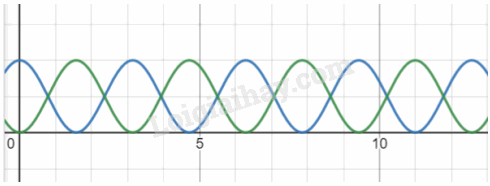
Thế năng của dao động là: \(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t-\dfrac{\pi}{2}\right)\)
Động năng của dao động là: \(W_d=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t-\dfrac{\pi}{2}\right)\)
Đường màu xanh lá cây là thế năng, đường màu xanh nước biển là động năng
Trên đồ thị những thời điểm mà hai đồ thị cắt nhau thì động năng và thế năng có độ lớn bằng nhau
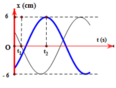

Vận tốc của vật vào thời điểm đó là: \(v=A\omega=\dfrac{2\pi A}{T}=\dfrac{2\pi\cdot10}{2}=10\pi\left(cm/s\right)\)