Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để tính vị trí của vật điều hoà tại thời điểm 1/3 giây sau khi vật có li độ x = 3cm, chúng ta cần tính giá trị của x tại thời điểm đó.
Phương trình vật dao động điều hoà đã cho là: x = 6cos(2πt - π/6) (cm)
Để tìm thời điểm 1/3s tiếp theo, ta thay t = 1/3 vào phương trình trên:
x = 6cos(2π(1/3) - π/6) = 6cos(2π/3 - π/6) = 6cos(π/2) = 6 * 0 = 0 (cm)
Vậy, tại thời điểm 1/3s tiếp theo, vật sẽ ở li độ x = 0cm.
Chu kì \(T=\dfrac{2\pi}{\omega}=0,5s\)
Trong thời gian 7/48s thì véc tơ quay đã quay một góc là:
\(\alpha=\dfrac{\dfrac{7}{48}}{0,5}.360=26,25^0\)
Biểu diễn dao động bằng véc tơ quay, ban đầu qua li độ \(2,5\sqrt 2\) và đang giảm
ứng với vị trí M như hình vẽ
M N
Lúc sau, véc tơ quay đến N, hình chiếu của N lên trục tọa độ sẽ cho biết li độ mới.
\(x=5.\cos(45-26,25)\approx4,73cm\)
@Thư Hoàngg: Bạn Quang Hưng nhầm trong việc tính góc α,
giá trị đúng phải là: \(\alpha = 105^0\), như vậy ban đầu véc tơ quay ở M quay 1050
sẽ đến N, khi đó ON tạo với Ox 1 góc là: 105 - 45 = 600
Suy ra: \(x=5.\cos(60^0)=2,5cm.\)
Đáp án D
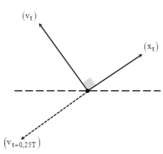
+ Biễu diễn vecto quay cho li độ x và vận tốc v của dao động. Lưu ý rằng tại cùng thời điểm t và v và x vuông pha nhau.
→ Vận tốc của vật tại thời điểm t + 0,25T ngược pha với li độ của vật tại thời điểm t.
→ Với hai đại lượng ngược pha, ta có:
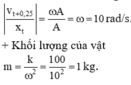
Đáp án D
Từ thời điểm t đến thời điểm t +
T
4
thì góc quay thêm là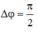 
ở thời điểm t + T 4
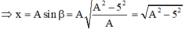luôn có
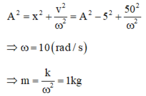
- Từ thời điểm t đến thời điểm t + T/4 thì góc quay thêm là: Δφ + π/2
- Ở thời điểm t + T/4:
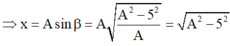
luôn có:
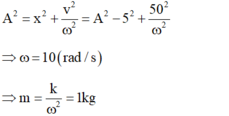
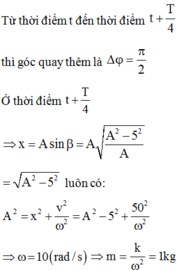
Gọi phương trình dao động \(x=A\cos\left(\omega t+\varphi\right).\left(1\right)\)
Chu kỳ T là thời gian thực hiện 1 dao động toàn phần.
=> \(T=\frac{\Delta t}{N}=\frac{100}{50}=2s.\)
=> \(\omega=\frac{2\pi}{T}=\pi.\)(rad/s)
Áp dụng công thưc mối quan hệ giữa li độ tức thời x, biên độ A và vận tốc tại vị trí li độ đó v là
\(A^2=x^2+\frac{v^2}{\omega^2}=20^2+\frac{\left(4\pi\sqrt{3}\right)^2}{\pi^2}=448\Rightarrow A=21,166cm.\)
Mình nghĩ bài của bạn số hơi xấu?:))))
Li độ tại thời điểm \(\left(t+\frac{1}{3}\right)s\) là
Bạn có 2 cách để làm thay t ở công thức (1) bằng t+1/3s.
Tuy nhiên mình hay dùng cách 2 đường tròn như sau
Thời điểm t vật có li độ 20 cm thêm 1/3 s nữa thì góc quay được là \(\varphi=\frac{1}{3}.\pi.\)
A 0 20 A 19 N M 10
Bài của bạn số xấu quá nên tìm góc cũng xấu.:))))))
\(\cos10^0=\frac{x}{A}\Rightarrow x=A\cos10^0\approx20,84cm.\)
à bài này thầy mình mới thay số lại =))) li độ bằng 4