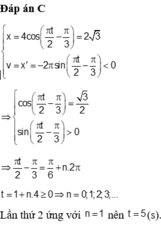Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lúc t=0 vật ở vị trí có li độ là A/2.
Do có yêu cầu chiều âm nên t2011=t1 + (2011-1)T
Từ A/2 theo chiều âm đến cân bằng là T/12 suy ra t2011= T/12+2010T=\(\frac{24121T}{12}\)
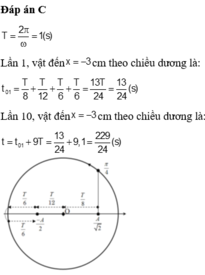
+ Biểu diễn dao động này bằng véc tơ quay.
+ Sau mỗi chu kì, chất điểm qua VTCB theo chiều âm 1 lần.
Như vậy, sau 2010 chu kì, chất điểm qua VTCB theo chiều âm là 2010 lần.
+ Lần cuối cùng véc tơ quay 1 góc 300 để đến VTCB theo chiều âm.
Như vậy, thời gian ở lần cuối là \(\dfrac{30}{360}T=T/6\)
Vậy, tổng thời gian là: \((2010+1/6).T\)

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)

Phương trình tổng quát: \(x= A cos(\omega t+\varphi)\)
+ Tần số góc: \(\omega = 2\pi/2 = \pi \ (rad/s)\)
+ t=0, vật qua VTCB theo chiều đương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ cm\\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình dao động: \(x = 5\cos(\pi t - \frac{\pi}{2})\) (cm)
tại sao lại ra φ=\(\dfrac{-\pi}{2}\) làm cách nào vậy bạn???

Tần số \(f=\dfrac{\omega}{2\pi}=2,5(hz)\)
Như vậy, khi biểu diễn dao động bằng véc tơ quay thì trong giây đầu tiên véc tơ quay đã quay 2,5 vòng.
O x M 6 3 4 N P
Véc tơ quay xuất phát từ M quay ngược chiều kim đồng hồ, trong giây đầu tiên, nó quay 2,5 vòng
Ta thấy nó qua N, P tổng cộng 4 lần nên dao động điều hòa qua x = 4cm 4 lần.

Phương trình tổng quát: x = \(A\cos(\omega t+\varphi)\)
+ Tần số: f= 120/60 = 2 Hz \(\Rightarrow \omega = 2\pi f = 2\pi .2 = 4\pi\) (rad/s)
+ Biên độ: A = 40/4 = 10 (cm) (1 chu kì vật đi quãng đường là 4A)
t=0, vật có li độ dương, chiều hướng về VTCB, nên v0<0.
\(\Rightarrow\left\{ \begin{array}{} x_0 = 5\ cm\\ v_0 <0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 5/10=0,5\ \\ \sin \varphi > 0 \end{array} \right. \Rightarrow \varphi = \frac{\pi}{3}\)
Vậy phương trình: \(x=10\cos(4\pi t +\frac{\pi}{3})\)