Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hệ kín, bảo toàn động lượng ta có: \(m_1v_1-m_2v_2=\left(m_1+m_2\right)v\)
\(\Leftrightarrow0,5.4-0,3.2=\left(0,5+0,3\right)v\)
\(\Leftrightarrow v=1,75\) m/s
Sau va chạm cả hai chuyển động cùng chiều với vật thứ nhất
Động lượng vật 1:
\(p_1=m_1\cdot v_1=0,5\cdot4=2kg.m\)/s
Động lượng vật 2:
\(p_2=m_2\cdot v_2=0,5\cdot2=1kg.m\)/s
Hai vật cđ ngược chiều bảo toàn động lượng:
\(m_1\cdot v_1-m_2\cdot v_2=\left(m_1+m_2\right)\cdot v\)
\(\Rightarrow2-1=\left(0,5+0,5\right)\cdot v\)
\(\Rightarrow v=1\)m/s

Chọn chiều \(\left(+\right)\) là chiều chuyển động của vật thứ nhất trước va chạm.
Trước va chạm
\(m_1=500g=0,5kg\) \(;\) \(v_1=+4m/s\)
\(m_2=300g=0,3kg\) \(;\) \(v_2=+0\) (Do trước va chạm vật đứng yên)
Sau va chạm
\(M=\left(m_1+m_2\right)=0,5+0,3=0,8kg\)
\(V=?m/s\)
==============================
Vì hệ kín, áp dụng định luật bảo toàn động lượng, ta có :
\(\overrightarrow{p_{trước}}=\overrightarrow{p_{sau}}\)
\(\Rightarrow m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=M\overrightarrow{V}\left(1\right)\)
Chiếu \(\left(1\right)\) lên chiều dương là chiều chuyển động của vật được chọn.
\(m_1v_1+m_2v_2=MV\)
\(\Leftrightarrow0,5.4+0,3.0=0,8.V\)
\(\Leftrightarrow0,8V=2\)
\(\Leftrightarrow V=+2,5\left(m/s\right)\)
Dấu \(+\) cho biết sau va chạm hai vật chuyển động cùng chiều chuyển động của vật thứ nhất trước va chạm.
Vậy vận tốc của 2 vật sau va chạm là \(2,5m/s\)

Động lượng vật thứ nhất:
\(p_1=m_1v_1=4m\) (g.m/s)
Động lượng vật thứ hai:
\(p_2=m_2v_2=3m\cdot3=9m\) (g.m/s)
Hai vật va chạm ngược chiều nhau. Bảo toàn động lượng:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\Rightarrow p=\left|p_1-p_2\right|=\left|4m-9m\right|=5m\)
Vận tốc của hai vật sau khi chuyển động là:
\(v=\dfrac{p}{m}=\dfrac{5m}{m_1+m_2}=\dfrac{5}{m+3m}=1,25\)m/s

Bảo toàn động lượng:
\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
Hai vật chuyển động ngược chiều nhau:
\(\Rightarrow-m_1v_1+m_2v_2=\left(m_1+m_2\right)\cdot v\)
\(\Rightarrow v=\dfrac{-2\cdot3+3\cdot5}{2+3}=1,8\)m/s

Chọn chiều dương là chiều chuyển động của vật 1 trước lúc va chạm
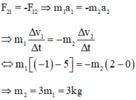

Chọn chiều dương là chiều của vật 1 chuyển động.
Áp dụng định luật bảo toàn động lượng :
\(\left(m_1+m_2\right)v=m_1.v_1-m_2.v_2\)
\(\Leftrightarrow v=\dfrac{m_1.v_1-m_2.v_2}{m_1+m_2}=-1,8\left(m\backslash s\right)\)
\(\Leftrightarrow\) Sau va chạm 2 vật chuyển động cùng chiều vật 2 ban đầu

Áp dụng công thức va chạm
v ' 1 = ( m 1 − m 2 ) v 1 + 2 m 2 m 2 m 1 + m 2 = ( 15 − 30 ) 22 , 5 − 2.30.18 45 = − 31 , 5 ( c m / s ) v ' 2 = ( m 2 − m 1 ) v 2 + 2 m 1 m 1 m 1 + m 2 = − ( 30 − 15 ) .18 + 2.15.22 , 5 45 = 9 ( c m / s )
Lưu ý: Khi thay số ta chọn chiều vận tốc v1 làm chiều (+) thì v2 phải lấy ( - ) và v2 = - 15 cm/s; vận tốc của m1 sau va chạm là v1 = - 31,5 cm/s. Vậy m1 chuyển động sang trái, còn m2 chuyển động sang phải.
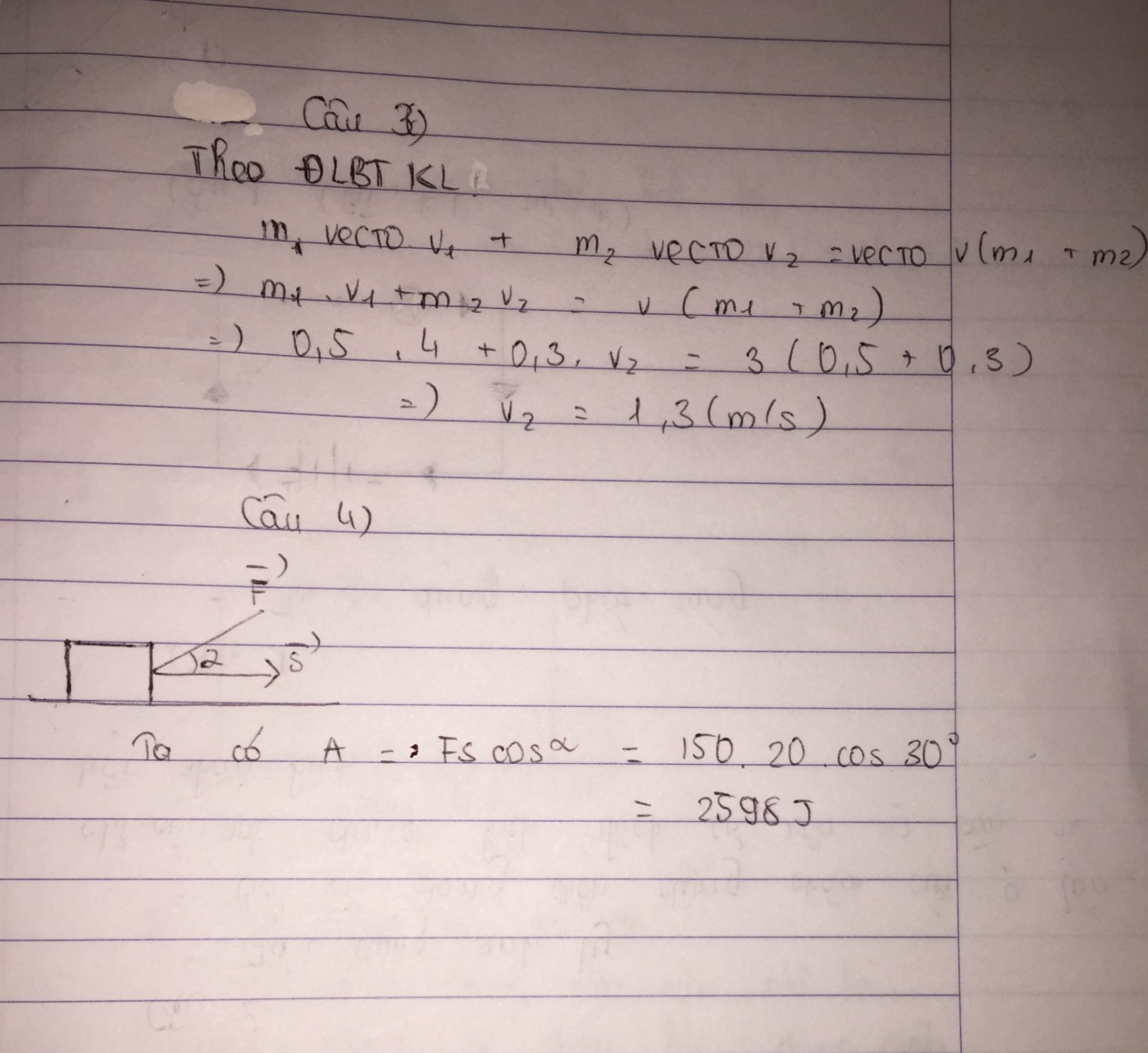
Đề bài nhìn dài làm đúng 2 dòng :))
Va chạm đàn hồi nên ta có :\(m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=m_1\overrightarrow{v_1'}+m_2\overrightarrow{v_2'}\)
\(\Leftrightarrow m_1v_1+m_2v_2=-m_1v_1'+m_2v_2'\)
\(\Leftrightarrow2.4+4.2=-2.1+4.v_2\Leftrightarrow v_2=4,5\left(m/s\right)\)