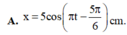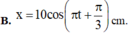Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

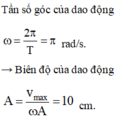
Ban đầu vật đi qua vị trí x = 0,5A = 5 cm theo chiều âm
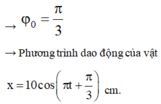
Đáp án C

Chọn C
+ ω = 2π : T = 20 rad/s.
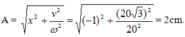
+ t = 0: x = 2cosφ = -1 => 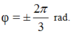
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.

Chọn C
Từ biểu thức tổng quát x = Acos(ωt + φ), ta tìm:
+ A: Quãng đường đi trong 1 chu kỳ là 4A => A = S/4 = 10cm
+ ω: Số dao động trong 1 giây: n = f = N t = 120 60 = 2 ( H z ) => ω = 2πf = 4π rad/s.
+ φ: t = 0 => x = A cosφ = 5; v = -Asinφ < 0 => φ = π/3 rad.
Vậy: x = 10 cos ( 4 πt + π 3 ) cm .

Câu 64: Một vật dao động điều hoà trên trục x’0x với chu kỳ T = 0,5s, Gốc toạ độ O là vị trí cân bằng của vật. Lúc t = 0 vât đi qua vị trí có li độ x = 3 cm, và vận tốc bằng 0. Phương trình dao động của vật:
A. x = 5cos(4π.t)(cm) B. x = 5cos(4π .t +π)(cm)
C. x = 3cos(4π.t +π)(cm) D. x = 3cos(4π.t)(cm)

Chọn A
+ Quãng đường đi trong một chu kỳ là 4A => A = 10cm.
+ w = 2 π T = π ( rad / s )
+ t = 0 => x = A cos φ = 0; v = -Asin φ > 0 => φ = -π/2
Vậy: x = 10 cos ( πt - π 2 ) cm.

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)

Đáp án C
Phương pháp: Sử dụng lí thuyết đại cương về dao động điều hòa
Cách giải:
Biên độ: A = 5cm
Tần số góc: ω = π rad/s.
Tại t = 0, vật qua VTCB theo chiều dương: φ = - π/2 (rad)
=> x = 5cos(πt – π/2) cm