Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đường thẳng d đi qua hai điểm \(\left( { - 1;1} \right)\) và \(\left( {2;3} \right)\) nên phương trình đường thẳng d là: \(\frac{{x + 1}}{{2 + 1}} = \frac{{y - 1}}{{3 - 1}} \Leftrightarrow 2x - 3y + 5 = 0\)
b) Phương trình đường tròn (C) có tâm \(I\left( {2;1} \right)\) và \(R = 2\) là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
c) Gọi \({d_1}\) là tiếp tuyến của đường tròn (C) tại điểm \(M\left( {2 + \sqrt 2 ;1 + \sqrt 2 } \right)\)
Ta có: \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {IM} = \left( {\sqrt 2 ;\sqrt 2 } \right)\). Vậy phương trình đường thẳng \({d_1}\) là:
\(\sqrt 2 \left( {x - 2 - \sqrt 2 } \right) + \sqrt 2 \left( {y - 1 - \sqrt 2 } \right) = 0 \Leftrightarrow x + y - 3 - 2\sqrt 2 = 0\)

Ta có tâm của đường tròn \(I(5;3)\)
Tiếp tuyến nhận vectơ \(\overrightarrow {IM} \) làm vectơ pháp tuyến nên ta có: \(\overrightarrow n = \overrightarrow {IM} = \left( {6;8} \right)\)
Điểm M nằm trên tiếp tuyến nên ta có phương trình:
\(6\left( {x - 11} \right) + 8\left( {y - 11} \right) = 0 \Leftrightarrow 3x + 4y - 77 = 0\)
Vậy phương trình tiếp tuyến của đường tròn \((C):{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 100\) tại điểm \(M(11;11)\) là \(3x + 4y - 77 = 0\)

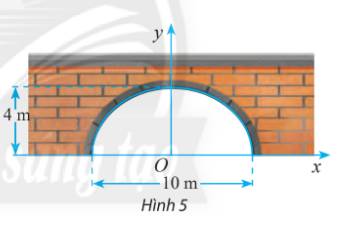
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 2} \right)\). Đường thẳng \(\Delta \) đi qua điểm \(N\left( {1;0} \right)\) nhận \(\overrightarrow {IN} = \left( {0;2} \right)\) làm vecto pháp tuyến là \(y = 0\).

Đường tròn có tâm \(I\left( {3; - 7} \right)\).
Phương trình tiếp tuyến tại điểm \(M\left( { - {\rm{ }}1{\rm{ }};--4} \right)\) thuộc đường tròn \({\left( {x - 3} \right)^2} + {\left( {y + 7} \right)^2} = 25\) là: \(\left( { - 1 - 3} \right)\left( {x + 1} \right) + \left( { - 4 + 7} \right)\left( {y + 4} \right) = 0 \Leftrightarrow - 4\left( {x + 1} \right) + 3\left( {y + 4} \right) = 0 \Leftrightarrow - 4x + 3y + 8 = 0\)

Tọa độ tiếp điểm là: \({M_1}\left( {3;5} \right),{M_2}\left( {3; - 12} \right)\)
Phương trình tiếp tuyến của đường tròn đi qua \({M_1}\) là: \( - 5\left( {x - 3} \right) - 12\left( {y - 5} \right) = 0 \Leftrightarrow - 5x - 12y + 75 = 0\)
Phương trình tiếp tuyến của đường tròn đi qua \({M_2}\) là:
\( - 5\left( {x - 3} \right) + 19(y + 12) = 0 \Leftrightarrow - 5x + 19y + 243 = 0\)

Lời giải:
Gọi PTTT đi qua $K(3;6)$ nên có dạng $(d):a(x-3)+b(y-6)=0(*)$ với $a^2+b^2\neq 0$
Gọi $I(1,2)$ là tâm đường tròn và $M$ là tiếp điểm của đường tiếp tuyến với đường tròn.
Ta có:
$IM=R=d(I,d)$
$\Leftrightarrow 3=\frac{|-2a-4b|}{\sqrt{a^2+b^2}}$
$\Rightarrow 5a^2-7b^2-16ab=0$
$\Rightarrow a=\frac{8+3\sqrt{11}}{5}b$ hoặc $a=\frac{8-3\sqrt{11}}{5}b$
Thay vô $(*)$ rồi rút gọn thì:
PTTT là:
$\frac{8+3\sqrt{11}}{5}x+y-\frac{54+9\sqrt{11}}{5}=0$
hoặc $\frac{8-3\sqrt{11}}{5}x+y-\frac{54-9\sqrt{11}}{5}=0$


Ta có \({\left( {\frac{{17}}{{12}} - 1} \right)^2} + {\left( {2 - 1} \right)^2} = \frac{{169}}{{144}}\), nên điểm M thuộc (C)
Đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\) có tâm \(I(1;1)\)
Phương trình tiếp tuyến d của (C) tại \(M\left( {\frac{{17}}{{12}};2} \right)\) là:
\(\begin{array}{l}\left( {\frac{{17}}{{12}} - 1} \right)\left( {x - \frac{{17}}{{12}}} \right) + \left( {2 - 1} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{5}{2}x + y - \frac{{133}}{{24}} = 0\end{array}\)