Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

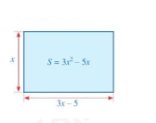
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)

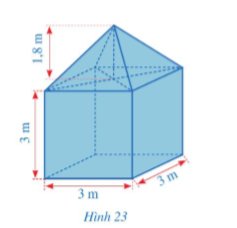
Thể tích của lều trại đó là.
\(V = {3^3} + \dfrac{1}{3}{3^2}.1,8 = 32,4({m^3})\)

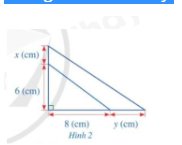
Diện tích hình tam giác vuông ban đầu là: \(\dfrac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Độ dài các cạnh của hình vuông sau khi tăng độ dài là: x + 6 (cm); y + 8 (cm)
Diện tích tam giác vuông sau khi tăng độ dài là: \(\dfrac{1}{2}\left( {x + 6} \right).\left( {y + 8} \right) = \dfrac{{{xy}}}{2} + 4x + 3y + 24\left( {c{m^2}} \right)\)
Đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y + 24 - 24 = \dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)
Vậy đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)

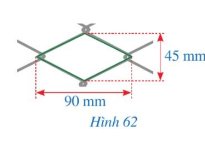
Giả sử mắt lưới cần tính độ dài cạnh là hình thoi ABCD.
Có. AC = 45mm; BD = 90mm.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi nên
\(\begin{array}{l}OA = OC = \dfrac{{AC}}{2} = \dfrac{{45}}{2} = 22,5(mm)\\OB = OD = \dfrac{{BD}}{2} = \dfrac{{90}}{2} = 45(mm)\end{array}\)
Xét \(\Delta AOB\) vuông tại O có:
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\{(22,5)^2} + {(45)^2} = A{B^2} \Rightarrow A{B^2} = 2.531,25 \Rightarrow AB \approx 50(mm)\end{array}\)

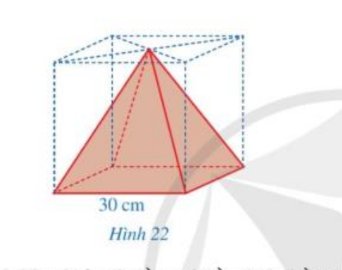
Thể tích của khối gỗ hình lập phương là:
\( V_{lp} = 30^3 = 27000 (cm^3)\)
Thể tích vật thể có hình chóp tứ giác đều là:
\(V_{hc} = \frac{1}{3}.30^2.30 = 9000 (cm^3)\)
Thể tích phần khúc gỗ bị cắt bỏ là:
\( V = V_{lp} - V_{hc} = 27000 - 9000 = 18000 (cm^3)\)
Vậy thể tích của phần khúc gỗ đã bị cắt bỏ là \(18000 cm^3\)

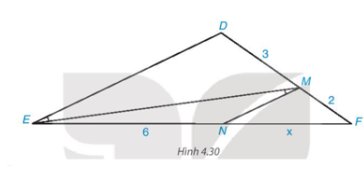
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

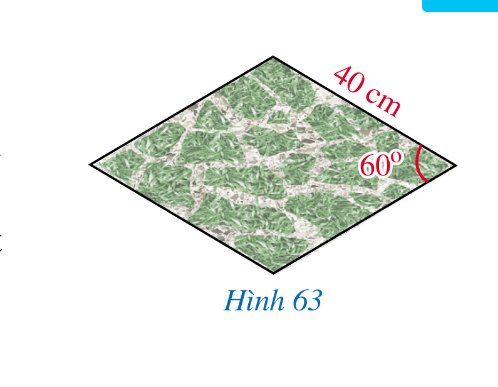
Giả sử viên gạch dạng hình thoi là hình thoi ABCD có.
AB = 40 cm; O là giao điểm của AC và BD
Xét \(\Delta DAB\) có: AB = AD = 40 cm; \( \Rightarrow \Delta DAB\) là tam giác đều suy ra
BD = AB = AD = 40cm \( \Rightarrow OB = \dfrac{{BD}}{2} = \dfrac{{40}}{2} = 20cm\)
Xét \(\Delta AOB\) vuông tại O có: \(O{A^2} + O{B^2} = A{B^2} \Rightarrow O{A^2} = A{B^2} - O{B^2} = {40^2} - {20^2} = 1200\)
\( \Rightarrow OA = \sqrt {1200} \Rightarrow AC = 2\sqrt {1200} \)
Diện tích của hình thoi ABCD là: \(S = \dfrac{1}{2}.AC.BD = \dfrac{1}{2}.40.2\sqrt {1200} = 1385,64(c{m^2})\)
Vậy diện tích của viên gạch đó là: \(1385,64(c{m^2})\)

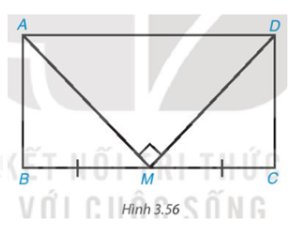
Do ABCD là hình chữ nhật nên \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\)
Mà M là trung điểm BC ⇒ \(\left\{{}\begin{matrix}MA=MD\\MB=MC\end{matrix}\right.\) (1)
Áp dụng định lí Py-ta-go trong tam giác ABM, MCD, AMD, ta có:
\(\left\{{}\begin{matrix}AB^2+MB^2=AM^2\\CD^2+MC^2=MD^2\\AM^2+MD^2=AD^2\end{matrix}\right.\) (2)
Từ (1) và (2), ta có:
\(2AB^2+2BM^2=AD^2=BC^2=4BM^2\)
\(\Rightarrow AB=BM=\dfrac{1}{2}BC\)
Mà \(2\cdot\left(AB+BC\right)=36\)
⇒ AB = 6 (cm) và BC = 12 (cm).
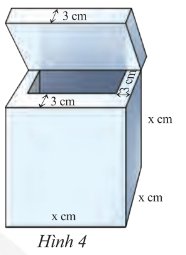
Sức chứa của thùng: `(x-3.2)^3 = (x-6)^3 = x^3 - 18x^2 + 108x - 216(cm^3)`.