Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do hứng được ảnh trên màn nên thấu kính đã sử dụng là thấu kính hội tụ.
b)
Đổi : \(AB=h=5\left(mm\right)=0,5\left(cm\right)\)
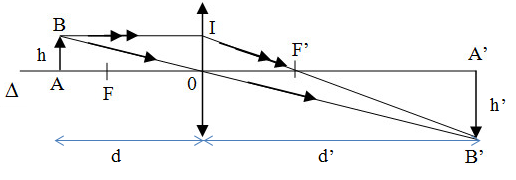
Xét \(\Delta OAB\sim\Delta OA'B'\) : \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\) (*)
Xét \(\Delta F'OI\sim\Delta F'A'B'\) : \(\dfrac{OI}{A'B'}=\dfrac{OF'}{F'A'}\).
Mà \(OI=AB\) và \(F'A'=OA'-OF'\) nên \(\dfrac{AB}{A'B'}=\dfrac{OF'}{OA'-OF'}\).
Từ đó, suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{OA'-OF'}\Leftrightarrow\dfrac{18}{d'}=\dfrac{12}{d'-12}\Leftrightarrow d'=36\left(cm\right)\)
Thay lại vào (*) ta được : \(\dfrac{18}{36}=\dfrac{0,5}{h'}\Leftrightarrow h'=1\left(cm\right)\)
Vậy : Ảnh ở vị trí cách thấu kính 36cm và cao 1cm.

MÌNH THAM KHẢO NHÉ
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

a) Dựng ảnh
O A B A' B' F I
b)
Xét các tam giác đồng dạng
IOF với A'B'F \(\Rightarrow \dfrac{IO}{A'B'}=\dfrac{OF}{B'F}\)
ABO với A'B'O \(\Rightarrow \dfrac{IO}{A'B'}=\dfrac{BO}{B'O}\)
Lại có: \(IO=AB\)
Từ đó bạn biến đổi tiếp nhé.

a. Dựng ảnh A'B'

b) d > f , ảnh lớn hơn và ngược chiều với vật
c)
Tóm tắt:
OF = 12cm
OA = 18cm
AB = 6cm
A'B' = ?
Giải:
Δ ABF ~ OIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{6}{A'B'}=\dfrac{18-12}{12}\)
=> A'B' = 12cm