Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

m2 = m1 = OA = 2OB = 2.8 = 16kg.
Vậy đầu B phải treo vật có khối lượng m2 là 16kg để thanh AB cân bằng.

Khi thanh cân bằng ta được phương trình:
\(m_1.OA=m_2.OB\)
\(\frac{m_1}{m_2}=\frac{OB}{OA}=\frac{OB}{2OB}=\frac{1}{2}\)
=> \(m_2=2m_1=2.8=16kg\)
Vậy phải treo ở đầu B một vật có khối lượng 16kg để thanh cân bằng.

Đáp án C
- Vì thanh nhẹ có thể quay quanh điểm O nên ta coi O là điểm tựa của đòn bẩy.
- Để hệ thống cân bằng ta có điều kiện cân bằng đòn bẩy như sau:
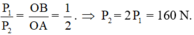
- Khối lượng vậy treo vào đầu B là:
160 : 10 = 16 (kg)
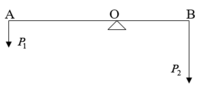

gọi l1 là chiều dài cánh tay đòn 1 ( ở đây là OA) l2 là chiều dài cánh tay đòn 2 ( ở đây là OB)
l1+l2=150 cm =1,5 m (1)
m1=3kg => P1=30(N)
m2=6kg => P2=60(N)
Để hệ thống cân bằng thì:
m1.l1=m2.l2
=> 30l1=60l2 => l1 - 2l2= 0 ( đơn giản mỗi vế cho 30) (2)
Từ (1) và (2) ta có hệ phương trình
l1+l2=1,5
l1 - 2l2=0
=> l1=1 (m)
l2=0,5(m)

giải
a) ta có: \(OA=40cm\)
\(\Rightarrow OB=AB-OA=160-40=120cm\)
trọng lượng của vật m1
\(P1=F1=10.m1=9.10=90\left(N\right)\)
áp dụng hệ thức cân bằng đòn bảy
\(\frac{F1}{F2}=\frac{l2}{l1}=\frac{OB}{OA}\)
lực tác dụng vào đầu B
\(F2=\frac{F1.OA}{OB}=\frac{90.40}{120}=30\left(N\right)\)
vậy để thanh AB được cân bằng thì phải treo vào đầu B một vật có khối lượng là \(\frac{30}{10}=3kg\)
b)ta có: \(OB=60cm\)
\(OA=AB-OB=160-60=100cm\)
áp dụng hệ thức cân bằng đòn bảy, để thanh AB cân bằng thì lực tác dụng vào đầu A
\(F'=\frac{F2.l2}{l1}=\frac{F2.OB}{OA}=\frac{30.60}{100}=18\left(N\right)\)
vậy vật m1=1,8kg tức là vật m1 phải bớt đi 7,2kg

Khi thanh cân bằng ta được phương trình:
m1.OA=m2.OB
⇒m1.2 OB=m2 .OB
⇒2m1=m2
⇒m2=2.8=16kg