Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì K là trung điểm BC nên B, K, C thẳng hàng theo thứ tự đó và BK = KC. Do vậy B', K', C' thẳng hàng theo thứ tự đó và B'K' = K'C', tức K' là trung điểm B'C'.
Vì G là trọng tâm tam giác ABC nên A, G, K thẳng hàng theo thứ tự đó và AG = 2GK. Do vậy A, G', K' thẳng hàng theo thứ tự đó và A'G' = 2G'K', tức G là trọng tâm tam giác A'B'C'.

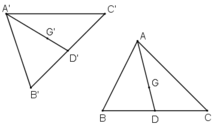
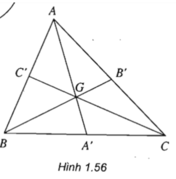
Gọi f là phép dời hình biến tam giác ABC thành tam giác A’B’C’.
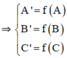
Gọi D là trung điểm của BC, D’ = f(D).
Gọi G là trọng tâm ΔABC, G’ = f(G).
+ B, D, C thẳng hàng ⇒ B’; D’; C’ thẳng hàng.
+ A; G; D thẳng hàng ⇒ A’; G’; D’ thẳng hàng.
+ B’D’ = BD = BC/2 = B’C’/2 ⇒ D’ là trung điểm B’C’.
+ A’G’ = AG = 2.AD/3 = 2.A’D’/3 ⇒ G’ là trọng tâm ΔA’B’C’.
Vậy phép dời hình f biến trọng tâm G của ΔABC thành trọng tâm G’ của ΔA’B’C’ (đpcm).

Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)

Tham khảo:
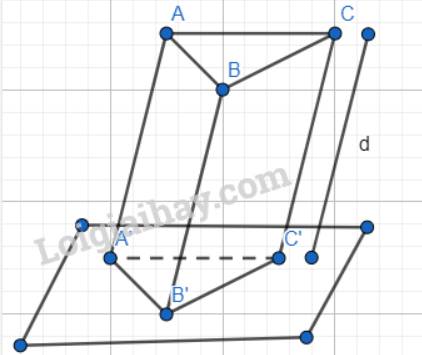
Nếu tam giác A′B′C′ là hình chiếu của tam giác ABC theo phương d thì tam giác ABC là hình chiếu của tam giác A′B′C′ vì tam giác ABC là tập hợp tất cả các hình chiếu của các điểm thuộc A'B'C' qua phép chiếu song song theo phương d.

Đáp án B
A’ = V G ; k ( A ) => − 2 G A ' → = G A → =>Tỉ số vị tự k = – 2

Theo đề bài ta có: AA', BB', CC' là các đường trung tuyến của ΔABC ⇒ G là trọng tâm
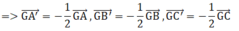
Vậy phép vị tự tâm G, tỉ số k = -1/2 biến tam giác ABC thành tam giác A'B'C'

A B C D M N P I K K X Y Z
a/
Ta có
M là trọng tâm tg ABC \(\Rightarrow\dfrac{MI}{MA}=\dfrac{1}{2}\)
N là trọng tâm tg ACD \(\Rightarrow\dfrac{NK}{NA}=\dfrac{1}{2}\)
Xét tg AIK có
\(\dfrac{MI}{MA}=\dfrac{NK}{NA}=\dfrac{1}{2}\) => MN//IK (Talet đảo trong tam giác)
Ta có
\(I\in BC;BC\in\left(BCD\right)\Rightarrow I\in\left(BCD\right)\)
\(K\in CD;CD\in\left(BCD\right)\Rightarrow K\in\left(BCD\right)\)
\(\Rightarrow IK\in\left(BCD\right)\) Mà MN//IK (cmt) => MN//(BCD)
Các trường hợp khác c/m tương tự
b/
Trong (ABC) từ M dưng đường thẳng // BC cắt AB; AC tại X và Y
Trong (ACD) nối YN cắt AD tại Z
Xét tg ABC có
\(\dfrac{XB}{XA}=\dfrac{YC}{YA}=\dfrac{MI}{MA}=\dfrac{1}{2}\) (Talet trong tam giác)
XY//BC; \(BC\in\left(BCD\right)\) => XY//(BCD)
Xét tg ACK có
\(\dfrac{YC}{YA}=\dfrac{NK}{NA}=\dfrac{1}{2}\) => YN//CK => YZ//CD
mà \(CD\in\left(BCD\right)\) => YZ//(BCD)
=> (XYZ)//(BCD)
Ta có MP//(BCD); MN//(BCD) => (MNP)//(BCD)
mà \(M\in\left(MNP\right);M\in\left(XYZ\right)\)
\(\Rightarrow\left(MNP\right)\equiv\left(XYZ\right)\) (Từ 1 điểm ngoài 1 mặt phẳng cho trước chỉ có duy nhất 1 mặt phẳng đi qua điểm đã cho và // với mặt phẳng cho trước)
=> (XYZ) là thiết diện của tứ diện ABCD khi cắt bởi (MNP)
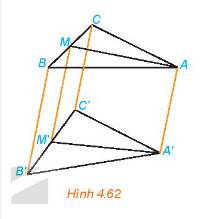

MN là đường trung bình của tam giác ABC
Vì M là trung điểm của BC nên B, M, C thẳng hàng theo thứ tự đó và \(\frac{{BM}}{{MC}} = 1\).
Do vậy, B’, M’, C’ thẳng hàng theo thứ tự đó và \(\frac{{B'M'}}{{M'C'}} = 1\).
Tức M’ là trung điểm của B’C’.
Tương tự, N’ là trung điểm của A’C’.
Vậy M’N’ là đường trung bình của tam giác A’B’C’.