Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi quãng đường AB là x ( km ) ( x>0 )
Thời gian đi là \(\dfrac{x}{25}\) (h)
Thời gian về là: \(\dfrac{x}{30}\) (h)
20 phút = 1/3 giờ
Theo đề bài ta có pt:
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{6x-5x}{150}=\dfrac{50}{150}\)
\(\Leftrightarrow x=50\left(tm\right)\)
Vậy quãng đường AB dài 50 km

20 phút = \(\dfrac{1}{3}\)h
Gọi quãng đường AB là x (km) (x > 0)
=> Thời gian xe máy từ A đến B với vận tốc 25km/h là: \(\dfrac{x}{25}\) h
Thời gian xe máy từ B về A với vận tốc 30km/h là: \(\dfrac{x}{30}\) h
Vì thời gian về ít hơn thời gian đi là \(\dfrac{1}{3}\)h
=> \(\dfrac{x}{25}\) - \(\dfrac{x}{30}\) = \(\dfrac{1}{3}\)
<=> \(\dfrac{6x-5x}{150}\) = \(\dfrac{1}{3}\) <=> \(\dfrac{x}{150}\) = \(\dfrac{1}{3}\)
<=> 3x = 150 <=> x = 50 (TMĐK)
Vậy quãng đường AB dài là 50 km

Gọi x là quãng đường AB (x >0,km)
Thời gian lúc đi là : x/40(h)
Thời gian lúc về là: x/30(h)
45 phút = 3/4 giờ
theo bài toán ta có phương trình
x/30-x/40 =3/4
<=> x(1/30-1/40) =3/4
<=> 1/120x=3/4
<=> x=90
Vậy quãng đường AB là 90km

Hiệu vận tốc của lúc đi và về là:
40 - 30 = 10 (km/h)
10 km/h ứng với 45 phút vậy quãng đường AB dài:
15 x (40 : 10) = 60 (km)
Đúng thì like

Gọi quãng đg ab là x (đk x>0)
Thời gian đi từ a - b là x/40(giờ)
thời gian về ừ b - a là x /30 (giờ)
45 p = 0,75 h
Theo bài ra ta có pt :
x /30 - x /40 = 0,75
=> 4x - 3x = 0,75 . 120
=> x = 90
Vậy AB là 90 km

Đổi \(45ph=\dfrac{3}{4}\left(h\right)\)
Gọi độ dài quãng đường AB là x>0 (km)
Thời gian đi: \(\dfrac{x}{40}\) giờ
Thời gian về: \(\dfrac{x}{30}\) giờ
Do thời gian về nhiều hơn thời gian đi 45ph nên ta có pt:
\(\dfrac{x}{30}-\dfrac{x}{40}=\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{x}{120}=\dfrac{3}{4}\)
\(\Rightarrow x=90\left(km\right)\)

Gọi độ dài quãng đường AB là x
Thời gian đi là x/45(h)
Thời gian về là x/30(h)
Theo đề, ta có x/30-x/45=1
hay x=90

Gọi x ( km ) là độ dài quãng đường AB ( x ∈ N* )
Thời gian người đó đi xe máy từ A đến B là: \(\dfrac{x}{30}\) ( giờ )
Thời gian người đó đi xe máy từ B đến A là: \(\dfrac{x}{25}\) ( giờ )
Vì thời gian người đó đi về nhiều hơn thời gian lúc đi 20 phút ( = \(\dfrac{1}{3}\) giờ ) nên ta có phương trình:
\(\dfrac{x}{30}+\dfrac{1}{3}=\dfrac{x}{25}\)
\(\dfrac{5x}{150}+\dfrac{50}{150}=\dfrac{6x}{150}\)
\(\Leftrightarrow5x+50=6x\)
\(\Leftrightarrow50=6x-5x\)
\(\Leftrightarrow50=x\) ( nhận )
Vậy quãng đường AB dài 50 km
Gọi \(x\left(km\right)\) là quãng đường AB \(\left(x>0\right)\)
Gọi thời gian người đó đi từ A đến B là \(\dfrac{x}{30}\left(h\right)\)
Gọi thời gian người đó đi từ B đến A là \(\dfrac{x}{25}\left(h\right)\)
Đổi \(20p=\dfrac{1}{3}h\)
Do lúc từ B về A người đó đi với vận tốc 25km/h nên thời gian về nhiều hơn thời gian đi 20 phút nên ta có pt :
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{90x-75x-2250}{2250}=0\)
\(\Leftrightarrow15x=2250\)
\(\Leftrightarrow x=150\left(n\right)\)
Vậy AB dài \(150km\)

Gọi độ dài quãng đường AB là x (km), (x > 0, km)
Thời gian đi từ A đến B: 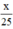 (giờ)
(giờ)
Thời gian đi từ B đến A: 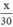 (giờ)
(giờ)
Thời gian về ít hơn thời gian đi 20 phút = 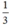 giờ nên ta có phương trình:
giờ nên ta có phương trình:
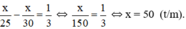
Vậy quãng đường AB dài 50km.
1. Đổi 20p = 1/3h
Gọi độ dài quãng đường AB là x (x > 0) (km)
Thời gian xe máy đi từ A đến B là x/25 (h)
Thời gian xe máy đi từ B về A là x/30 (h)
Theo bài ra ta có: x/25 - x/30 = 1/3
<=> 5x/750 = 1/3
<=> x/150 = 1/3
<=> x = 50 (TM)
Vậy quãng đường AB dài 50km