


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Giả sử khoảng cách AB = d (km).
Gọi vận tốc của người đi bộ là x km/h, x > 0.
Theo đầu bài, người đi ngựa đi quãng đường AB hết 5/6 giờ. Do đó vận tốc của người đi ngựa là d: 5/6 = 6d/5 (km).
Người đi ngựa đến trước người đi bộ 5/6 giờ. Điều đó có nghĩa là
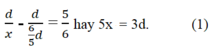
Từ đó cũng suy ra 6d/5 = 2x; nghĩa là vận tốc của người đi ngựa là 2x km/h. Vì người đi ngựa khi quay lại gặp người đi bộ ở điểm cách B một khoảng là 2km nên:
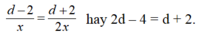
Từ (1) và (2), ta có hệ phương trình 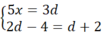
Giải hệ này ta được d = 6, x = 3,6.
Vậy: Khoảng cách AB = d = 6 km,
Vận tốc của người đi bộ là 3,6 km/h,
Vận tốc của người đi ngựa là 7,2 km/h.

Gọi khoảng cách giữa hai bản A và B là x (km)
Vận tốc của người đi bộ là y (km/h)
Điều kiện: x > 0; y > 0
Người đi ngựa cả đi và về hết 1 giờ 40 phút =53=53 giờ nên người đi ngựa đi từ A đến B hết 53:2=5653:2=56 giờ.
Vận tốc của người đi ngựa bằng x:56=65xx:56=65x (km/h)
Thời gian người đi bộ đi hết quãng đường AB là xyxy giờ
Người đi ngựa đến trước 50 phút =56=56 giờ, ta có phương trình:
xy−56=56⇔3x=5yxy−56=56⇔3x=5y (1)
Từ (1) ⇒ 6x=10y⇔65x=2y.6x=10y⇔65x=2y. Điều này có nghĩa là vận tốc người đi ngựa gấp đôi người đi bộ nên vận tốc người đi ngựa là 2y (km/h).
Từ lúc đi đến lúc gặp nhau người đi bộ đi được x – 2 (km), người đi ngựa đi được x + 2 (km).
Vì từ lúc đi đến lúc gặp thời gian hai người bằng nhau, ta có phương trình:
x−2y=x+22y⇔2x−4=x+2x−2y=x+22y⇔2x−4=x+2
Ta có hệ phương trình:
{3x=5y2x−4=x+2⇔{3x=5yx=6⇔{3.6=5yx=6⇔{x=6y=3,6{3x=5y2x−4=x+2⇔{3x=5yx=6⇔{3.6=5yx=6⇔{x=6y=3,6
x = 6 và y = 3,6 thỏa mãn điều kiện bài toán.
Vậy khoảng cách giữa hai bản là 6km
Vận tốc người đi bộ là 3,6 km/h
Vận tốc người đi ngựa là 7,2 km/h

Gọi vận tốc của người đi xe máy trên 3/4 quãng đường AB đầu (90 km) là x (km/h) (x > 0)
Vận tốc của người đi xe máy trên 1/4 quãng đường AB sau là 0,5x (km/h)
Vận tốc của người đi xe máy khi quay trở lại A là x + 10 (km/h)
Tổng thời gian của chuyến đi là 90 x + 30 0 , 5 x + 120 x + 10 + 1 2 = 8 , 5
⇔ 90 x + 60 x + 120 x + 10 = 8 ⇔ 150 x + 120 x + 10 = 8 ⇔ 75 ( x + 10 ) + 60 x = 4 x ( x + 10 ) ⇔ 4 x 2 − 95 x − 750 = 0 ⇔ x = 30 ( d o x > 0 )
Vậy vận tốc của xe máy trên quãng đường người đó đi từ B về A là 30 + 10 = 40 (km/h)

gọi qd tu A den B la S ta co pt;
s/50+ (s - 20) /50 - 1/4 =(s-20)/40 + 1/4
s=? hieu k?