Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a.
Chu vi hình chữ nhật: $2(x+y)$ (m)
Diện tích hình chữ nhật: $xy$ (m2)
b.
Chiều rộng: $12-2=10$ (m)
Chu vi: $2(x+y)=2(12+10)=44$ (m)
Diện tích: $12\times 10=120$ (m2)

Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là \(a,b\left(m\right),a>b>0\).
Chu vi là \(30m\)nên \(2\left(a+b\right)=30\Leftrightarrow a+b=15\Leftrightarrow a=15-b\)
Diện tích là \(54m^2\)nên \(ab=54\Leftrightarrow b\left(15-b\right)=54\)
\(\Leftrightarrow\orbr{\begin{cases}b=6\Rightarrow a=9\left(tm\right)\\b=9\Rightarrow a=6\left(l\right)\end{cases}}\)
Tỉ số chiều dài và chiều rộng là: \(\frac{a}{b}=\frac{9}{6}=\frac{3}{2}\).

\(1,\\ Cd=0,55:\left(3+2\right)\cdot3=0,33\left(m\right)\\ \Rightarrow S_{\text{vườn cây}}=0,33\left(0,55-0,33\right)=0,0726\left(m^2\right)\\ 2,\text{Nửa cv là: }57,5:2=28,75\left(m\right)\\ \Rightarrow Cd=28,75:\left(1+3\right)\cdot3=21,5626\left(m\right)\\ \Rightarrow S_{\text{mảnh vườn}}=21,5626\left(28,75-21,5626\right)\approx154,98\left(m^2\right)\)

a, Nửa chu vi mảnh vườn:
50:2=25(m)
Chiều dài bằng 1,5 chiều rộng (sửa đề vậy mới đúng nha). Nên chiều dài = 3/2 chiều rộng
Tổng số phần bằng nhau:
2+3=5(phần)
a, Chiều dài mảnh vườn:
25:5 x 3= 15(m)
Chiều rộng mảnh vườn:
25-15=10(m)
b, Diện tích mảnh vườn:
15 x 10 = 150(m2)
Đ.số: a, chiều dài 15m và chiều rộng 10m
b, Diện tích 150m2
a) Nữa chi vi hình chữ nhật:
\(50:2=25\left(m\right)\)
Ta có: \(1,5=\dfrac{3}{2}\)
Tổng số phần bằng nhau:
\(3+2=5\) (phần)
Chiều rộng:
\(25:5\times2=10\left(m\right)\)
Chiều dài:
\(25-10=15\left(m\right)\)
b) Diện tích mảnh vườn:
\(15\times10=150\left(m^2\right)\)

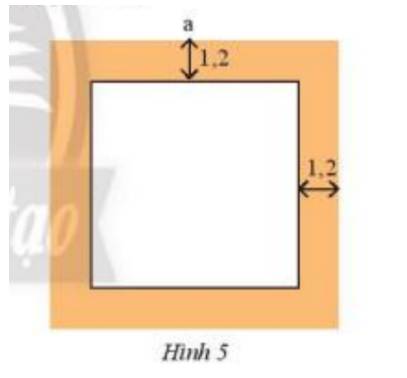
1 cạnh của mảnh vườn còn lại là : a – 1,2 – 1,2 = a – 2,4 (m)
Diện tích mảnh vườn còn lại có biểu thức tính là : \({(a - 2,4)^2}\) (\({m^2}\))
Thay a = 20 vào biểu thức ta vừa tính được :
\({(20 - 2,4)^2}\)\( = 309,76 ({m^2}\))

a: \(S=xy\left(m^2\right)\)
b: Diện tích phần vườn để trồng rau là \(xy-5\cdot2=xy-10\left(m^2\right)\)

a) Gọi độ dài 2 cạnh hình chữ nhật là x ,y (m) (x, y > 0)
Vì tỉ số giữa độ dài hai cạnh của nó bằng \(\frac{3}{5}\) nên \(\frac{x}{y} = \frac{3}{5} \Rightarrow \frac{x}{3} = \frac{y}{5}\)
Vì chu vi của mảnh đất là 48 m nên 2.(x+y) = 48 nên x + y = 48:2= 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\frac{x}{3} = \frac{y}{5} = \frac{{x + y}}{{3 + 5}} = \frac{{24}}{8} = 3\\ \Rightarrow x = 3.3 = 9;y = 5.3 = 15\end{array}\)
Vậy chiều dài, chiều rộng của mảnh vườn đó lần lượt là: 15m và 9m.
b) Diện tích hình chữ nhật là: S = 9.15 = 135 (m2)
tham khảo:
a) Gọi chiều dài và chiều rộng của mảnh vườn hình chữ nhật lần lượt là x và y (m) (x > y > 0).
Nửa chu vi mảnh vườn là:48 : 2 = 24 (m)
Khi đó ta có: x + y = 24 (m).
Vì tỉ số độ dài giữa hai cạnh của mảnh vườn bằng \(\dfrac{3}{5}\) nên \(\dfrac{y}{x}=\dfrac{3}{5}\) hay \(\dfrac{y}{3}\)=\(\dfrac{x}{5}\) (tính chất tỉ lệ thức).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{3}\)=\(\dfrac{x+y}{5+3}\)=\(\dfrac{24}{8}\)=3
Khi đó:
+) \(\dfrac{x}{5}\)=3 suy ra x = 5.3 = 15 (thoả mãn);
+) \(\dfrac{y}{3}=3\) suy ra y = 3.3 = 9 (thoả mãn).
Khi đó chiều dài mảnh vườn là 15 m; chiều rộng mảnh vườn là 9 m.
b) Diện tích mảnh vườn là:
15.9 = 135 (m2).
Vậy diện tích mảnh vườn là 135 (m2).

tổng chiều dài và chiều rộng là 30:2 =15m
gọi x là chiều dài , ta có chiều rộng là 15-x m
diện tích mảnh vườn là : \(x\left(15-x\right)=54\)\(\Leftrightarrow x^2-9x-6x+54=0\Leftrightarrow\left(x-6\right)\left(x-9\right)=0\Leftrightarrow\orbr{\begin{cases}x=6\\x=9\end{cases}}\)
vì x là chiều dài nên x=9 và chiều rộng afl 6 m
tỉ số chiều dài và chiều rộng là : \(\frac{9}{6}=\frac{3}{2}\)
a: Nửa chu vi mảnh vườn là 90:2=45(m)
Chiều rộng mảnh vườn là 45-x(m)
Diện tích mảnh vườn là \(x\left(45-x\right)=45x-x^2\left(m^2\right)\)
b: Khi x=30 thì diện tích mảnh vườn là:
\(45\cdot30-30^2=1350-900=450\left(m^2\right)\)
a) Nửa chu vi mảnh vườn là 90:2=45(m)
Chiều rộng mảnh vườn là 45-x(m)
Diện tích mảnh vườn là:
x (45 - x) = 45x - x² (m²)
b) Khi x = 30 thì diện tích mảnh vườn là:
46 • 30 - 30² = 1350 - 900 = 450 (m²)
Vậy ...