Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Phương pháp: Sử dụng giản đồ vecto
Cách giải:
Vì điện áp hai đầu cuộn dây sớm pha π/2 so với điện áp hai đầu mạch nên trong cuộn dây có điện trở r
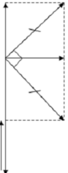
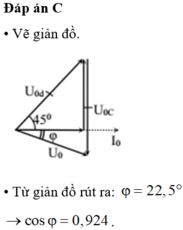
Vì điện áp hiệu dụng của cuộn dây bằng điện áp hiệu dụng đặt vào 2 đầu mạch, lại lệch pha nhau π/2, dựa vào hình vẽ ta thấy tam giác ABO là tam giác vuông cân.
Tức là
Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$
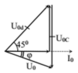
Ta có Ud=UC Mà ta có \(_{ }\varphi_d\)=π/4 ..Từ hình vẽ thấy : cos \(\varphi_d\)= \(\frac{\sqrt{2}}{2}=\frac{U_r}{U_d}\) → Ur=\(\frac{1}{\sqrt{2}}\)Ud
Có U2= Ud2+ Ud2 -- 2 Ud.Ud.cos 45 → U= Ud.\(\sqrt{2-\sqrt{2}}\)
Hình vẽ → cos\(\varphi_m\)= \(\frac{Ur}{U}\)= \(\frac{\frac{1}{\sqrt{2}}}{\sqrt{2-\sqrt{2}}}\) = 0,924
Ud Uc=Ud UL Ur U
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm một cuộn dây mắc nối tiếp với một tụ
điện. Điện áp hiệu dụng giữa hai đầu cuộn dây có giá trị bằng điện áp hiệu dụng giữa hai bản tụ điện.
Dòng điện tức thời trong đoạn mạch chậm pha pi/4 so với điện áp tức thời giữa 2 đầu cuộn dây. Hệ số công suất của đoạn mạch là
A. 0,707. B. 0,866. C. 0,924. D. 0,999.
Chọn đáp án B
Đặt U d = 1 V → U C = 2 V
u d và u C lệch pha nhau góc α = 3π/4 → U = U d 2 + U C 2 + 2 U d U C cos α = 1 V
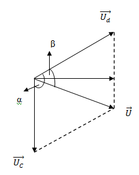
Vẽ giản đồ véc tơ như hình vẽ, gọi β là góc lệch giữa u d và u
→ cosβ = U d 2 + U 2 − U C 2 2 U d U = 0 → β = π/2.
Chọn đáp án B
Đặt 
lệch pha nhau góc α = 3π/4 → U 
= 1 V
Vẽ giản đồ véc tơ như hình vẽ, gọi β là góc lệch giữa Ud và u
→ cosβ =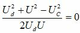 
→ β = π/2.
