Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C.
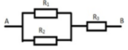
Để hoạt động tốt, mạch điện có thẻ có các trường hợp sau:
TH1: 1 tốt, 2 tốt,3 tốt, 4 tốt: P1 = 0,8.0,9.0,95.0,98 = 0,67032
TH2: 1 tốt, 2 tốt,3 cháy, 4 tốt: P1 = 0,8.0,9.0,05.0,98 = 0,03528
TH3: 1 tốt, 2 cháy,3 tốt, 4 tốt: P1 = 0,8.0,1.0,95.0,98 = 0,07448
Từ đó xác suất để mạch hoạt động tốt là 0,67032 + 0,03528 + 0,07448 = 0,78008
Gọi xác suất bộ phận 1 bị hỏng là x với \(0\le x\le1\)
Xác suất không bị hỏng của 2 bộ phận lần lượt là \(1-x\) và \(0,2\)
Xác suất có đúng 1 bộ phận bị hỏng (gồm 2 TH1: 1 hỏng 2 bình thường, 1 bình thường 2 hỏng):
\(x.0,2+\left(1-x\right).0,8=0,38\)
\(\Rightarrow x=0,7\)
Trả lời:
a) Vận tốc của chuyển động khi t = 2 (s).
Ta có:
v=dsdt=S′=3t2−6t−9v=dsdt=S′=3t2−6t−9
Khi t = 2(s) ⇒ 3.22 – 6.22 – 9 = -9 m/s.
b) Gia tốc của chuyển động khi t = 3(s). Ta có:
a=dvdt=v′=6t−6a=dvdt=v′=6t−6
Ở t = 3(s) ⇒ a = 6.3 – 6 = 12 m/s2
c) Ta có: v = 3t2 – 6t – 9
Tại thời điểm vận tốc triệt tiêu:
v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)
Gia tốc: a = 6t – 6.
Khi t = 3s ⇒ a = 6.3 – 6 = 12 m/s2
d) Ta đã có a = 6t – 6.
Khi a = 0 ⇔ 6t – 6= 0 ⇔ t = 1(s)
Lại có: v = 3t2 – 6t – 9
Khi t = 1(s) ⇒ v = 3.12 – 6.1 – 9 = -12 m/s
a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến t + ∆t là
vtb = =
=
g .(2t + ∆t) ≈ 4,9. (2t + ∆t).
Với t = 5 và
+) ∆t = 0.1 thì vtb ≈ 4,9. (10 + 0,1) ≈ 49,49 m/s;
+) ∆t = 0,05 thì vtb ≈ 4,9. (10 + 0,05) ≈ 49,245 m/s;
+) ∆t = 0,001 thì vtb ≈ 4,9. (10 + 0,001) ≈ 49,005 m/s.
b) Vận tốc tức thời của chuyển động tại thời điểm t = 5s tương ứng với ∆t = 0 nên v ≈ 4,9 . 10 = 49 m/s.
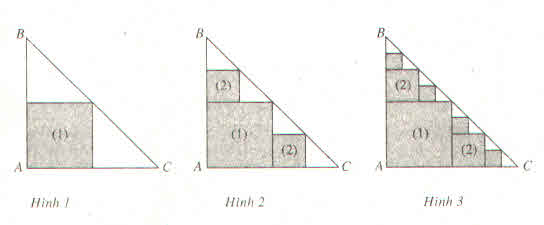
a) Hình vuông thứ nhất có cạnh bằng nên u1 = (
)2 =
.
Hình vuông thứ hai có cạnh bằng nên u2 = (
)2 =
.
Hình vuông thứ ba có cạnh bằng nên u3 = (
)2 =
.
Tương tự, ta có un =
b) Dãy số (un) là một cặp số nhân lùi vô hạn với u1 = và q =
. Do đó
lim Sn = .
a) Cần biết ít nhật ba trong năm đại lượng u1, n, d, un, Sn thì có thể tính được hai đại lượng còn lại.
b) Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng. Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.
b1) Biết u1 = -2, un = 55, n = 20. Tìm d, Sn
Áp dụng công thức d =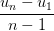 
, Sn =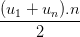 
Đáp số: d = 3, S20 = 530.
b2) Biết d = -4, n = 15, Sn = 120. Tìm u1, un
Áp dụng công thức un = u1 + (n - 1)d và Sn = ,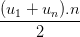
ta có: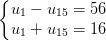 
Giải hệ trên, ta được u1 = 36, u15 = - 20.
Tuy nhiên, nếu sử dụng công thức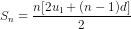 
thì S15 = 120 = 15u1 +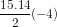 
.
Từ đó ta có u1 = 36 và tìm được u15 = - 20.
b3) Áp dụng công thức un = u1 + (n - 1)d, từ đây ta tìm được n; tiếp theo áp dụng công thức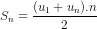 
. Đáp số: n = 28, Sn = 140.
b4) Áp dụng công thức 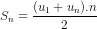, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: u1 = -5, d= 2.
b5) Áp dụng công thức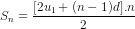 
, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: n = 10, un = -43
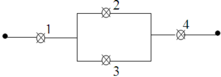
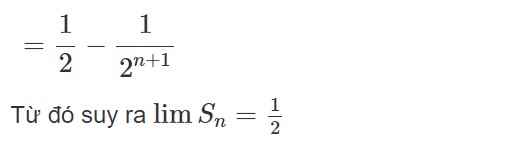
Xác suất để linh kiện 1 hoạt động tốt là: 1-0,2=0,8
Xác suất để linh kiện 2 hoạt động tốt là: 1-0,1=0,9
Xác suất để linh kiện 3 hoạt động tốt là: 1-0,05=0,95
Lưu ý rằng khi mắc mạch song song, linh kiện 1 hỏng thì linh kiện 2 vẫn hoạt động tốt và ngược lại.
Xác suất để cả 3 linh kiện hoạt động tốt là: 0 , 8.0 , 9.0 , 95 = 0 , 684
Xác suất để linh kiện 1 hỏng, 2 linh kiện còn lại hoạt động tốt là: 0 , 2.0 , 9.0 , 95 = 0 , 171
Xác suất để linh kiện 2 hỏng, 2 linh kiện còn lại hoạt động tốt là: 0 , 8.0 , 1.0 , 95 = 0 , 076
Vậy xác suất để mạch hoạt động được là: 0 , 684 + 0 , 171 + 0 , 076 = 0 , 931
Chọn đáp án A.