Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số kết quả thuận lợi cho biến cố \(A \cup B\) là \(5 + 12 = 17\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{{n\left( \Omega \right)}};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega\right)}} = \frac{{12}}{{n\left( \Omega\right)}};P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega\right)}} = \frac{{17}}{{n\left( \Omega\right)}}\)
\( \Rightarrow P\left( A \right) + P\left( B \right) = P\left( {A \cup B} \right)\)

Ta có n(Ω) = 40
a) Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8
Chọn đáp án là C

Ta có n(Ω) = 40
b) Rõ ràng n(B) = 10 nên P(B) = 10/40 =1/4
Chọn đáp án B

Ta có n(Ω) = 40
c) Nhận thấy :
![]()
![]()
Mà P(A∪B) = P(A) + P(B) –P(A∩B), A∩B là biến cố:”học sinh được chọn giỏi cả Văn và Toán” nên n(A∩B)=5/40=1/8
![]()
![]()
Chọn đáp án C
Nhận xét:
ở ý a) và b) học sinh có thể nhầm khi quan niệm: chọn 1 học sinh nên n(A) =n(B) =1 ⇒ phương án A; hoặc chọn 1 học sinh trong 5 học sinh giỏi Toán và Văn nên n(A) =n(B) = 5
⇒ P(A) =P(B) =5/40=1/8 (phương án D); hoặc sử dụng nhầm công thức P(A) =(n(Ω))/(n(A))=8/3;P(B)=(n(Ω))/(n(B))=4 (phương án C)
ở ý c), học sinh có thể nhầm khi quan niệm:
![]()
![]()
![]()
Nhưng A ¯ v à B ¯ không phải là hai biến cố độc lập

![]()
Có thể giải ý c) cách khác như sau:
Số học sinh giỏi Văn và Toán gồm: học sinh giỏi Văn, học sinh hioir Toán, học sinh giỏi cả Văn và Toán nên bằng (15 +10) -5 = 20 em. Do đó, số học sinh không giỏi cả Toán và Văn là 40 – 20 = 20 em, nên n(C) = 20
Vì vậy P(C) =(n(C))/(n(Ω))=1/2

\(P\cup Q\): Học sinh đó hoặc bị cận thị hoặc giỏi môn toán
PQ: Học sinh đó vừa bị cận thị vừa giỏi môn Toán
\(\overline{PQ}\): Học sinh đó vừa không bị cận thị vừa không giỏi môn Toán

a) Không gian mẫu của bài toán này là tập hợp các học sinh trong tổ lớp, nó có 9 phần tử và được ký hiệu là Ω = {Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}.
b) Biến cố H xảy ra khi học sinh được chọn là một bạn nữ, nó là tập hợp các học sinh nữ và được ký hiệu là
H = {Hương, Hồng, Dung, Phương}.
Biến cố K xảy ra khi học sinh được chọn có tên bắt đầu là chữ cái H, được ký hiệu là
K = {Hương, Hồng, Hoàng}.
Biến cố hợp M xảy ra khi học sinh được chọn là một bạn nữ hoặc có tên bắt đầu bằng chữ H, nó là tập hợp các học sinh trong tập H hoặc K (bao gồm cả những học sinh trùng nhau của hai tập này) và được ký hiệu là
M = H ∪ K = {Hương, Hồng, Dung, Phương, Hoàng}.
a: Ω={Hương, Hồng, Dung, Phương, Sơn, Tùng, Hoàng, Tiến, Hải}
n(Ω)=9
b: H={Hương, Hồng, Dung, Phương}
K={Hương, Hồng, Hoàng}
=>M={Hương,Hồng,Dung,Phương,Hoàng}
H là tập con của M và Ω
K là tập con của M và Ω
M là tập con của Ω
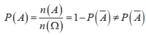
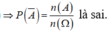
tham khảo
a) Số kết quả thuận lợi cho biến cố A là \(C^3_{17}=680\)
Số kết quả thuận lợi cho biến cố B là \(C^2_{17}.C^1_{15}=2040\)
b)\(A\cup B\) là biến cố "Có ít nhất 2 học sinh nữ trong 3 học sinh được chọn"Số kết quả thuận lợi cho biến cố \(A\cup B\) là:\(680+2040=2720\)