Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

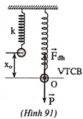
a) Khi m ở vị trí cân bằng O: P → + F d h → = 0 →
Về độ lớn: m g - k x 0 = 0 1
Trong đó x0 là độ giãn lò xo khi vật ở vị trí cân bằng (hình 91). Xét khi m chuyển động, ở vị trí cách O một đoạn x. Thế năng của hệ sẽ bằng công do trọng lực và lực đàn hồi thực hiện khi m di chuyển từ vị trí đang xét trở về vị trí ban đầu ( tức là trở về vị trí cân bằng O).
Ta có:
![]()
hay
![]()
Từ (1) và (2)
![]()
b) Tại vị trí ban đầu ta có
![]()

Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...


Ở vị trí cân bằng lực đàn hồi cân bằng với trọng lực nên: ![]()
Vì chọn mốc thế năng của hệ tại vị trí cân bằng O tức là tại đó tổng thế năng đàn hồi và thế năng trọng lực bằng O, nên:
![]()
Thế năng của vật tại A gồm thế năng đàn hồi và thế năng trọng lực.
Thế năng đàn hồi:
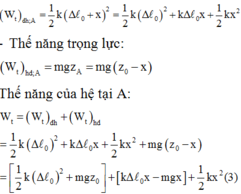
Thay (1) và (2) vào (3) ta được:

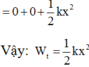

a) Độ biến dạng của lò xo là:
\(\Delta l=l-l_0=22-20=2\left(cm\right)=0,02cm\)
Ta có: \(P+F=0\) (ở vị trí cân bằng)
\(\Rightarrow P=F\)
Mà \(P=mg\) và \(F=k\Delta l\)
\(\Rightarrow mg=k\Delta l\)
\(\Leftrightarrow k=\dfrac{mg}{\Delta l}\)
\(\Leftrightarrow k=\dfrac{0,5.10}{0,02}\)
\(\Leftrightarrow k=250N/m\)
b) Độ dài lò xo dãn ra:
Ta có: \(P=F\)
\(\Leftrightarrow\left(m_1+m_2\right).g=k.\Delta l\)
\(\Leftrightarrow\Delta l=\dfrac{\left(m_1+m_2\right).g}{k}\)
\(\Leftrightarrow\Delta l=\dfrac{\left(0,5+0,3\right).10}{250}=0,032\left(m\right)=3,2\left(cm\right)\)
Chiều dài của lò xo:
\(l=\Delta l+l_0=3,2+20=23,2\left(cm\right)\)

Lời giải
Ta có độ biến dạng của lò xo so với vị trí ban đầu: Δl=10cm=0,1
=> Thế năng đàn hồi của lò xo tại vị trí đó: W t = 1 2 k Δ l 2 = 1 2 .200. 0 , 1 2 = 1 J
Đáp án: C

a/ \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}k\Delta l^2\)
\(\Leftrightarrow kx^2+mv^2=k\Delta l^2\Leftrightarrow v=\sqrt{\dfrac{k\Delta l^2-kx^2}{m}}=\sqrt{\dfrac{40.0,02^2-40x^2}{0,4}}\left(m/s\right)\)
b/ \(v_{max}\Leftrightarrow\dfrac{40.0,02^2-40x^2}{0,4}\left(max\right)\Leftrightarrow x=0\) => khi nó ở VTCB
\(\Rightarrow v_{max}=\dfrac{40.0,02^2}{0,4}\left(m/s\right)\)
 10
10

