Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

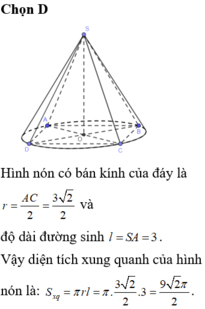
Đáp án D.
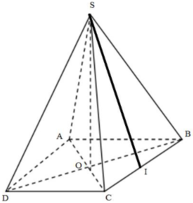
Phương pháp:
+) Gọi b là độ dài cạnh bên, sử dụng giả thiết diện tích xung quanh gấp đôi diện tích đáy biểu diễn b theo a.
+) Gọi O = AC ∩ BD ⇒ SO ⊥ (ABCD)
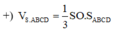
Cách giải:
Gọi b là độ dài cạnh bên, I là trung điểm của BC ⇒ SI ⊥ BC
Tam giác SIB vuông tại I
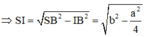
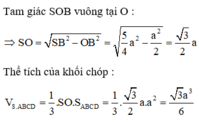

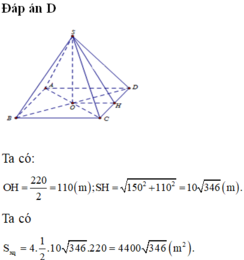
Đáp án là D
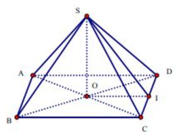
Thể tích khối chóp
Gọi O là tâm của hình vuông, I là trung điểm DC thì SI ⊥ CD .
Đặt SO = h. Có
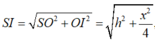
![]()
Suy ra:
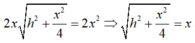
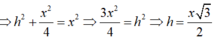
Lúc đó:
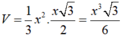

Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


Đáp án là D
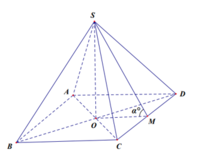
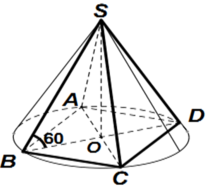
+) Gọi độ dài cạnh đáy là x, gọi M là trung điểm của CD, O ≡ AC ∩ BD.
=> ((SCD);( ABCD)) = SMO= α .
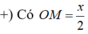
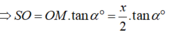
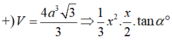
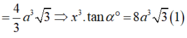
+) Theo giả thiết
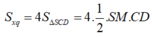
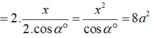
![]()
+) Từ (1) và (2) ta có hệ:
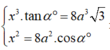
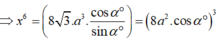
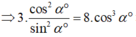
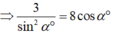
![]()
![]()
![]()
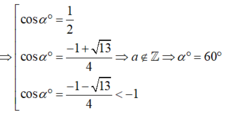
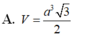
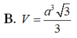
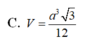
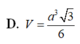

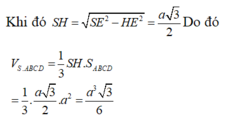
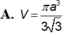

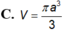
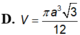
Lời giải:
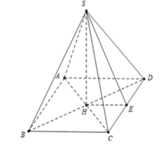
Xét hình chóp tứ giác đều $S.ABCD$ thì $ABCD$ là hình vuông có cạnh bằng 10 và các cạnh bên bằng nhau.
Gọi độ dài cạnh bên là $a$.
Từ $S$ hạ đường cao $SH$ xuống hình chóp thì $H$ chính là tâm của hình vuông $ABCD$
Theo định lý Pitago: \(AC=\sqrt{AB^2+BC^2}=\sqrt{10^2+10^2}=10\sqrt{2}\)
\(AH=\frac{1}{2}AC=5\sqrt{2}(dm)\)
Tiếp tục áp dụng định lý Pitago:
\(SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-50}\)
Do đó \(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\sqrt{a^2-50}.100\)
Xét tam giác cân $SAB$ có đáy $AB=10$, hai cạnh $SA=SB=a$
Theo công thức Herong diện tích của tam giác là: \(\sqrt{p(p-a)(p-a)(p-10)}\) trong đó \(p=\frac{a+a+10}{2}=a+5\)
\(\Rightarrow S_{SAB}=5\sqrt{a^2-25}\)
\(\Rightarrow S_{xq}=20\sqrt{a^2-25}\)
Do \(V_{S.ABCD}=S_{xq}\Rightarrow \frac{100\sqrt{a^2-50}}{3}=20\sqrt{a^2-25}\)
Giải pt trên ta thu được \(a=\frac{5\sqrt{41}}{4}\) (dm)
Do đó:
Chiều cao hình chóp: \(SH=\sqrt{a^2-50}=\frac{15}{4}\) (dm)
\(S_{xq}=V=20\sqrt{a^2-25}=125\)
Pn cho mk cái hình vẽ đc hok . Để hỉu hơn ấy :))