Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Số cách chọn một bạn nam và một bạn nữ để hát song ca là C 6 1 . C 4 1 = 24

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2 = 210 cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1 = 35 cách chọn
Suy ra xác suất cần tính bằng
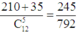

Chọn B.
Không gian mẫu có số phần tử là ![]() .
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: ![]() .
.
Vậy xác suất cần tính là 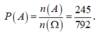 .
.

Đáp án C
Phương pháp:
Sử dụng quy tắc nhân
Để chọn được nhóm có một bạn nam và một bạn nữ ta làm như sau:


Khi đó, số cách chọn hai bạn sao cho có một bạn nam và một bạn nữ là:
![]()

Chọn A
Số cách chọn một bạn nam là 12 cách.
Số cách chọn một bạn nữ là 10 cách
Vậy số cách chọn hai bạn trực nhật có cả nam và nữ là 12.10 = 120 (cách)

a. Chọn bất kì 5 học sinh từ 50 học sinh có: \(C_{50}^5\) cách
b. Lớp có 20 học sinh nam. Chọn 5 bạn trong đó có 2 bạn nam (suy ra 3 bạn nữ) đồng nghĩa: chọn 2 nam từ 20 nam và 3 nữ từ 30 nữ
\(\Rightarrow\) Có \(C_{20}^2.C_{30}^3\) cách
c. Số cách chọn 5 bạn toàn là nữ: \(C_{30}^5\) cách
Số cách chọn 5 bạn có ít nhất 1 nam: \(C_{50}^5-C_{30}^5\) cách

Lời giải:
a) Chọn một đội gồm $12$ người từ $15+10=25$ người có số cách chọn là: \(C^{12}_{25}\)
b) Bạn xem lại đề.
Số cách chọn thỏa mãn yêu cầu là \(C_{10}^2.C_{10}^3=5400\) cách.