Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiều cao của cột cờ là:
\(10.5\cdot tan\left(35^045'\right)\simeq7,56\left(m\right)\)

Bài 2
 a) ∆ABC vuông tại A, AH là đường cao
a) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.HC
= 4.9
= 36
⇒ AH = 6 (cm)
BC = BH + HC
= 4 + 9 = 13 (cm)
∆ABC vuông tại A, AH là đường cao
⇒ AB² = BH.BC
= 4.13
= 52 (cm)
⇒ AB = 2√13 (cm)
⇒ cos ABC = AB/BC
= 2√13/13
⇒ ∠ABC ≈ 56⁰
b) ∆AHB vuông tại H, HE là đường cao
⇒ AH² = AE.AB (1)
∆AHC vuông tại H, HF là đường cao
⇒ AH² = AF.AC (2)
Từ (1) và (2) suy ra:
AE.AB + AF.AC = 2AH² (3)
Xét tứ giác AEHF có:
∠HFA = ∠FAE = ∠AEH = 90⁰ (gt)
⇒ AEHF là hình chữ nhật
⇒ AH = EF (4)
Từ (3) và (4) suy ra:
AE.AB + AF.AC = 2EF²
Bài 1
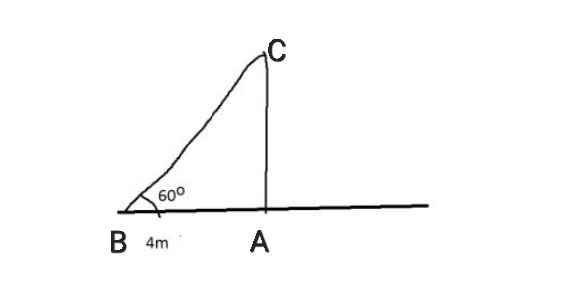 Ta có:
Ta có:
tan B = AC/AB
⇒ AC = AB . tan B
= 4 . tan60⁰
= 4√3 (m)
≈ 7 (m)

A B C 4,8 3,5
Có: \(\tan C=\frac{AB}{AC}=\frac{3,5}{4,8}\)
=> \(\widehat{C}=36^o\)
Vậy ................
Vì tan = đối / kề => kề = đối/tan
Chiều cao cột cờ là :
9/ tan 42 = xấp xỉ 10 m